| Codeforces Round 566 (Div. 2) |
|---|
| Закончено |
Дерево состоит из $$$n$$$ вершин. Выберите одну вершину как корень. Он должен удовлетворять условию ниже.
- Для каждой пары вершин $$$v_{1}$$$ и $$$v_{2}$$$, если $$$distance$$$($$$root$$$, $$$v_{1}$$$) $$$= distance$$$($$$root$$$, $$$v_{2})$$$, тогда $$$degree$$$($$$v_{1}$$$) $$$= degree$$$($$$v_{2}$$$), где $$$degree$$$ — количество смежных вершин, а $$$distance$$$ — количество ребер между двумя вершинами.
Определите и найдите, есть ли такой корень в дереве. Если есть несколько ответов, выведите любой из них.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 10^{5}$$$) — количество верши.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$v_{i}$$$ и $$$u_{i}$$$ ($$$1 \le v_{i} \lt u_{i} \le n$$$), которые значат, что существует ребра между вершинами $$$v_{i}$$$ и $$$u_{i}$$$. Гарантируется, что граф — дерево.
Если такой корень существует, выведите любой из них. Иначе выведите $$$-1$$$.
7 1 2 2 3 3 4 4 5 3 6 6 7
3
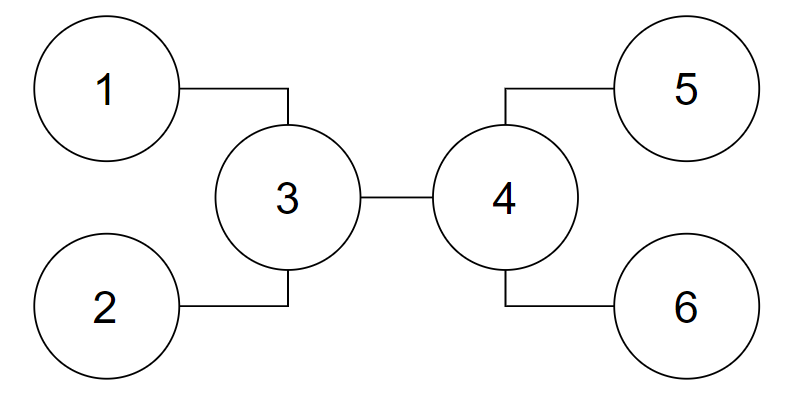
6 1 3 2 3 3 4 4 5 4 6
-1
Рисунок до первого примера. $$$1$$$, $$$5$$$, $$$7$$$ — также могут быть корнями.
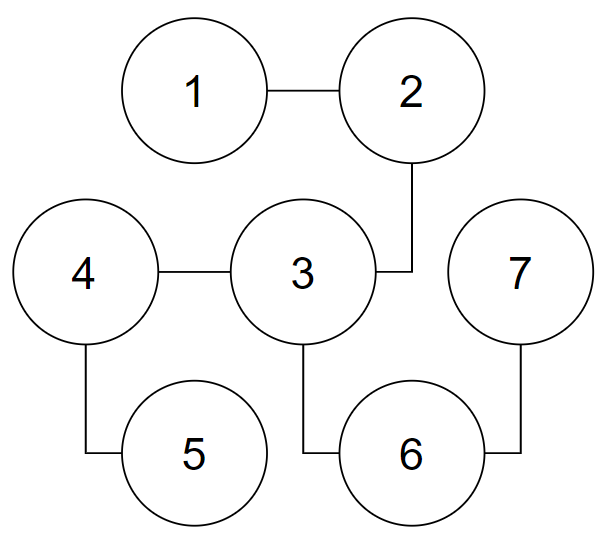
Рисунок до второго примера. Невозможно найти корень графа.
| Название |
|---|




