Киберлюди снова перехитрили Далеков! К сожалению, на этот раз Далеки решили отказаться от этих задач вообще, а значит, Доктору придётся ими заняться.
Доктор может справиться с Далеками самостоятельно, но Хайди теперь должна убедиться, что Киберлюди заняты вот этой, следующей задачей.
На плоскости задано $$$k$$$ колец. Для каждого кольца, выбирается $$$n$$$ случайных точек на нём с небольшим случайным шумом. Задачей является восстановление колец на основе зашумлённых точек.
Кольца и точки генерируются следующим образом. Центер кольца генерируется равновероятно из диска с радиусом $$$1\,000\,000$$$ с центром в начале координат, а радиус кольца равновероятно выбирается из $$$[250\,000, 750\,000]$$$. Пусть $$$R$$$ это кольцо с центром $$$(x, y)$$$ и радиусом $$$r$$$. Чтобы выбрать точку в кольце $$$R$$$ выбирается угол $$$\theta$$$ равновероятно из $$$[0, 2\pi]$$$ и расстояние $$$d$$$ из $$$[0.9r, 1.1r]$$$. Координаты генерируемой точки тогда $$$(x+d\cos(\theta), y+d\sin(\theta))$$$, округлённые к ближайшим целым числам.
Расстояние между кольцами измеряется с помощью расстояния Хаусдорфа. В нашем случае, расстояние между кольцами $$$R_1, R_2$$$ может быть записано следующим образом. Пусть $$$d$$$ является расстоянием между двумя центрами, а $$$r_1, r_2$$$ являются радиусами. Тогда расстояние равно:
$$$$$$dist(R_1, R_2)=\max(\min(d_{--}, d_{-+}),\min(d_{+-}, d_{++}), \min(d_{--}, d_{+-}), \min(d_{-+}, d_{++}))$$$$$$, где $$$d_{++}=|d+r_1+r_2|$$$, $$$d_{+-}=|d+r_1-r_2|$$$, $$$d_{-+}=|d-r_1+r_2|$$$, $$$d_{--}=|d-r_1-r_2|$$$.
Скажем, что кольцо $$$R_0$$$ успешно восстановлено, если одно из колец $$$R$$$ в выводе находится на расстоянии Хаусдорфа не более чем $$$100\,000$$$ от $$$R_0$$$.
Вывод вашей програмы будет засчитан, если все кольца успешно восстановлены. Гарантируется, что расстояние между любыми двумя кольцами превышает $$$600\,000$$$.
Помните, что любой человек может легко решить эту задачу, так что убедитесь, что ни один человеческий предатель не помогает Киберлюдям решить эту задачу.
Первая строка содержит одно целое число $$$k$$$ ($$$1 \leq k \leq 4$$$) — количество колец.
Вторая строка содержит одно целое число $$$n$$$ ($$$100 \leq n \leq 1\,000$$$) — количество точек на одно кольцо.
Каждая из следующих $$$n \times k$$$ строк задаёт точки, по одной точке в строке.
Каждая из них содержит пару целых чисел $$$x_i, y_i$$$, где $$$(x_i, y_i)$$$ это координаты $$$i$$$-й точки.
Выведите $$$k$$$ строк, по одному кольцу на строку.
В каждой строке выведите три вещественных числа $$$x_i, y_i, r_i$$$, где $$$(x_i, y_i)$$$ и $$$r_i$$$ это координаты $$$i$$$-го кольца и его радиус.
Порядок колец не имеет значения.
Один из тестов с $$$k=4$$$ и $$$n=100$$$ выглядит следующим образом.
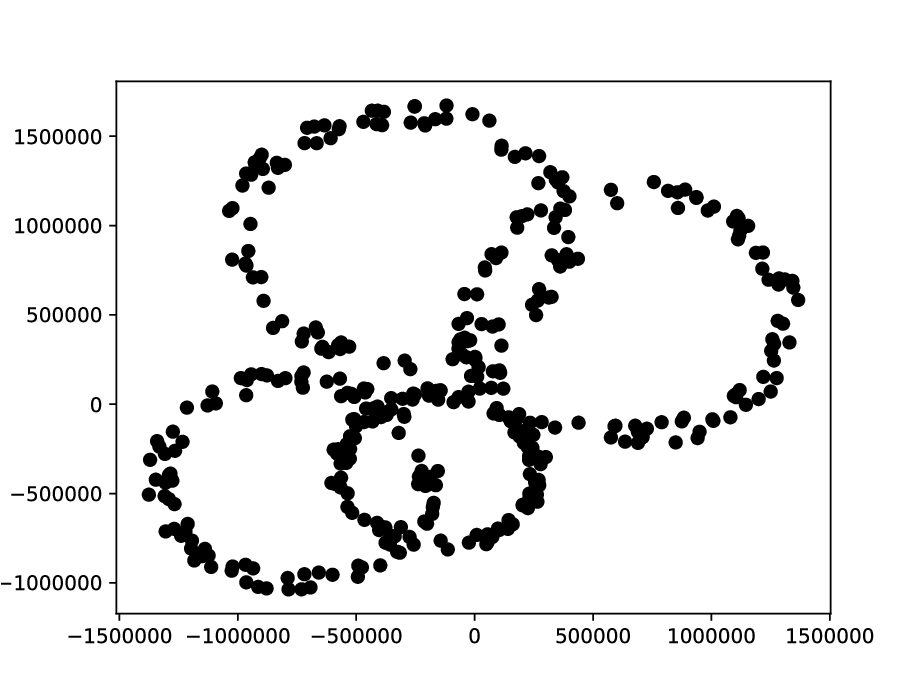
Вы можете скачать пример здесь.
| Название |
|---|




