Вам задано дерево (неориентированный связный ацикличный граф), состоящее из $$$n$$$ вершин. Вы играете в игру на этом дереве.
Изначально все вершины белые. На первом ходу игры Вы выбираете одну вершину и красите ее в черный. Затем на каждом ходу Вы выбираете белую вершину, смежную (соединенную ребром) с любой черной вершиной и красите ее в черный.
Каждый раз, когда вы выбираете вершину (даже во время первого хода), Вы получаете количество очков, равное размеру компоненты связности, состоящей только из белых вершин, содержащей выбранную вершину. Игра заканчивается, когда все вершины покрашены в черный цвет.
Рассмотрим следующий пример:
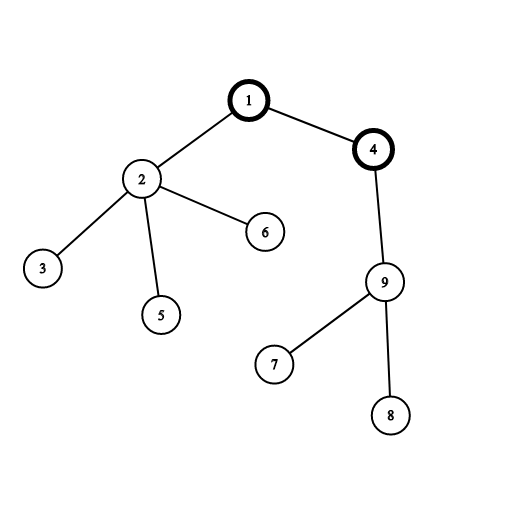
Вершины $$$1$$$ и $$$4$$$ уже покрашены в черный цвет. Если Вы выберете вершину $$$2$$$, Вы получите $$$4$$$ очка за компоненту связности, состоящую из вершин $$$2, 3, 5$$$ и $$$6$$$. Если Вы выберете вершину $$$9$$$, Вы получите $$$3$$$ очка за компоненту связности, состоящую из вершин $$$7, 8$$$ и $$$9$$$.
Ваша задача — максимизировать количество очков, которое Вы получите.
Первая строка содержит одно целое число $$$n$$$ — количество вершин в дереве ($$$2 \le n \le 2 \cdot 10^5$$$).
Каждая из следующих $$$n - 1$$$ строк описывает ребро дерева. Ребро $$$i$$$ описывается двумя целыми числами $$$u_i$$$ и $$$v_i$$$, номерами вершин, которые оно соединяет ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$).
Гарантируется, что заданные ребра образуют дерево.
Выведите одно целое число — максимальное количество очков, которое вы получите, если будете играть оптимально.
9 1 2 2 3 2 5 2 6 1 4 4 9 9 7 9 8
36
5 1 2 1 3 2 4 2 5
14
Первый тестовый пример показан в условии задачи.
| Название |
|---|




