| Codeforces Round 572 (Div. 2) |
|---|
| Закончено |
Вам дано $$$n$$$ чисел $$$a_1, a_2, \ldots, a_n$$$. Возможно ли расставить их по окружности таким образом, чтобы каждое число было строго меньше суммы своих соседей?
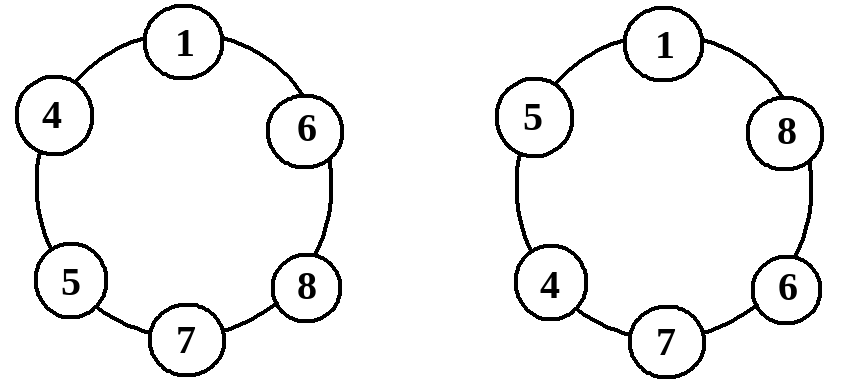
К примеру, для массива $$$[1, 4, 5, 6, 7, 8]$$$, расстановка слева удовлетворяет условию, в то время как расстановка справа нет, так как $$$5\ge 4 + 1$$$ и $$$8> 1 + 6$$$.
Первая строка содержит одно целое число $$$n$$$ ($$$3\le n \le 10^5$$$) — количество чисел.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \leq a_i \le 10^9$$$) — сами числа. Заданные числа не обязательно различны.
Если решения не существует, в первой строке выведите «NO».
Если оно существует, в первой строке выведите «YES». После чего, во второй строке выведите $$$n$$$ чисел — элементы массива в порядке в котором они будут стоять на окружности. Первый и последний элементы, которые вы выведете, считаются соседями на окружности. Если существует несколько решений, выведите любое из них. Вы можете выводить круг, начиная с любого из чисел.
3 2 4 3
YES 4 2 3
5 1 2 3 4 4
YES 4 4 2 1 3
3 13 8 5
NO
4 1 10 100 1000
NO
Одна из возможных расстановок указана в первом примере:
$$$4< 2 + 3$$$;
$$$2 < 4 + 3$$$;
$$$3< 4 + 2$$$.
Одна из возможных расстановок указана в втором примере.
При любой расстановке чисел $$$13, 8, 5$$$ на окружности в третьем примере, $$$13$$$ будет иметь соседей $$$8$$$ и $$$5$$$, но $$$13\ge 8 + 5$$$.
В четвертом примере нет нужной расстановки.
| Название |
|---|




