| Codeforces Round 578 (Div. 2) |
|---|
| Закончено |
Гильдон проводит эксперименты с интересной машиной под названием Graph Traveler. В этой машине есть ориентированный граф из $$$n$$$ вершин, пронумерованных от $$$1$$$ до $$$n$$$. $$$i$$$-я вершина имеет $$$m_i$$$ выходящих ребер, они обозначаются $$$e_i[0]$$$, $$$e_i[1]$$$, $$$\ldots$$$, $$$e_i[m_i-1]$$$, где каждый элемент обозначает номер вершины конца ребра. В графе могут быть кратные ребра и петли. Кроме того, в каждой вершине $$$i$$$ написано некоторое целое число $$$k_i$$$.
Путь по графу определяется следующим образом.
- Гильдон выбирает вершину, с которой начнет путь, а также некоторое начальное целое число. Запомним это число в переменную $$$c$$$.
- Когда Гильдон приходит в вершину $$$i$$$, а также, в начале, если путь начинается с вершины $$$i$$$, он добавляет значение $$$k_i$$$ к $$$c$$$.
- Следующая вершина пути — это $$$e_i[x]$$$, где $$$x$$$ — такое целое число $$$0 \le x \le m_i-1$$$, что $$$x \equiv c \pmod {m_i}$$$. Гильдон переходит в эту следующую вершину и возвращается на шаг 2.
Ясно, что такой путь никогда не кончается, потому что шаги 2 и 3 будут повторяться бесконечное число раз.
Например, предположим, что Гильдон начинает в вершине $$$1$$$ с $$$c = 5$$$, при этом $$$m_1 = 2$$$, $$$e_1[0] = 1$$$, $$$e_1[1] = 2$$$, $$$k_1 = -3$$$. Сразу после того, как он начинает в вершине $$$1$$$, $$$c$$$ становится равным $$$2$$$. Так как единственное целое число $$$x$$$ ($$$0 \le x \le 1$$$) такое, что $$$x \equiv c \pmod {m_i}$$$, это $$$0$$$, то Гильдон пойдет в вершину $$$e_1[0] = 1$$$. После того как он попадет в вершину $$$1$$$ снова, $$$c$$$ станет равной $$$-1$$$. Единственное целое число $$$x$$$, удовлетворяющее сравнению, есть $$$1$$$, поэтому он идет в вершину $$$e_1[1] = 2$$$, и так далее.
Так как Гильдон достаточно любознательный, он хочет спросить у вас $$$q$$$ вопросов. Каждый раз он хочет узнать, сколько различных вершин он посетит бесконечное число раз, если он начнет с определенной вершины с определенным числом $$$c$$$. Обратите внимание, что не нужно учитывать вершины, которые будут посещены только конечное число раз.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 1000$$$) — количество вершин в графе.
Вторая строка содержит $$$n$$$ целых чисел. $$$i$$$-е из них равно $$$k_i$$$ ($$$-10^9 \le k_i \le 10^9$$$) — число, написанное в $$$i$$$-й вершине.
Следующие $$$2 \cdot n$$$ строк описывают ребра, выходящие из каждой вершины. $$$(2 \cdot i + 1)$$$-я строка содедржит одно целое число $$$m_i$$$ ($$$1 \le m_i \le 10$$$) — число исходящих ребер из вершины $$$i$$$. $$$(2 \cdot i + 2)$$$-я строка содержит $$$m_i$$$ целых чисел $$$e_i[0]$$$, $$$e_i[1]$$$, $$$\ldots$$$, $$$e_i[m_i-1]$$$, все значения которых лежат в пределах от $$$1$$$ до $$$n$$$ включительно.
Следующая строка содержит одно целое число $$$q$$$ ($$$1 \le q \le 10^5$$$) — количество вопросов Гильдона.
Каждая из следующих $$$q$$$ строк содержит два целых числа $$$x$$$ и $$$y$$$ ($$$1 \le x \le n$$$, $$$-10^9 \le y \le 10^9$$$), которые означают, что Гильдон хочет начать путь с вершины $$$x$$$, а начальное значение переменной $$$c$$$ должно быть $$$y$$$.
Для каждого запроса выведите количество различных вершин, которые будут посещены бесконечно много раз, если Гильдон начнет путь из вершины $$$x$$$ с начальным значением $$$y$$$.
4 0 0 0 0 2 2 3 1 2 3 2 4 1 4 3 1 2 1 6 1 0 2 0 3 -1 4 -2 1 1 1 5
1 1 2 1 3 2
4 4 -5 -3 -1 2 2 3 1 2 3 2 4 1 4 3 1 2 1 6 1 0 2 0 3 -1 4 -2 1 1 1 5
1 1 1 3 1 1
Граф в первом примере показан на рисунке ниже:
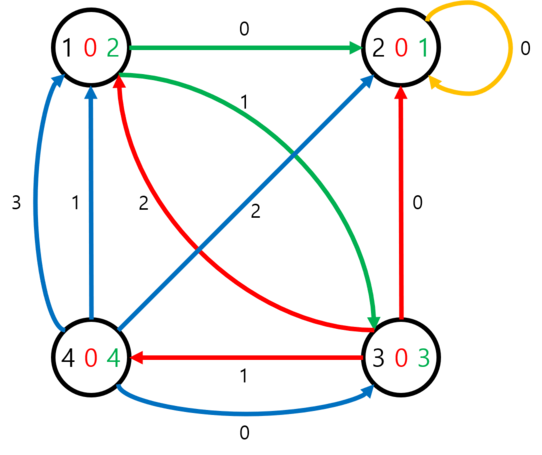
Три числа, показанные на вершине $$$i$$$, равны соответственно $$$i$$$, $$$k_i$$$ и $$$m_i$$$. Числа на ребрах показывают их номер в списке выходящих ребер из $$$i$$$-й вершины.
Путь для каждого запроса показан ниже. Он описывается последовательностью фраз, каждая в формате «вершина ($$$c$$$ после добавления $$$k_i$$$)».
- $$$1(0) \to 2(0) \to 2(0) \to \ldots$$$
- $$$2(0) \to 2(0) \to \ldots$$$
- $$$3(-1) \to 1(-1) \to 3(-1) \to \ldots$$$
- $$$4(-2) \to 2(-2) \to 2(-2) \to \ldots$$$
- $$$1(1) \to 3(1) \to 4(1) \to 1(1) \to \ldots$$$
- $$$1(5) \to 3(5) \to 1(5) \to \ldots$$$
Во втором примере граф такой же, как в первом, но у вершин ненулевые значения. Поэтому ответы отличаются от ответов в первом примере.
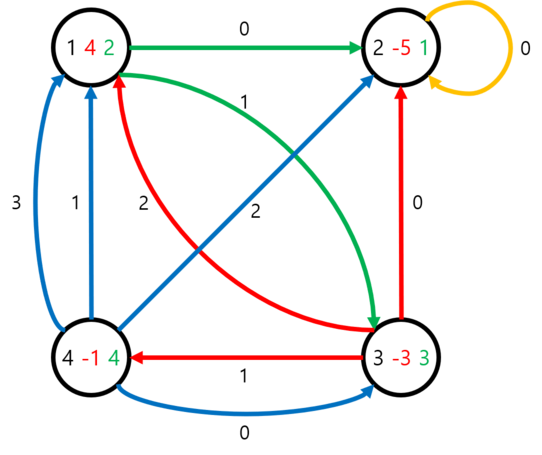
Пути во втором примере показаны ниже:
- $$$1(4) \to 2(-1) \to 2(-6) \to \ldots$$$
- $$$2(-5) \to 2(-10) \to \ldots$$$
- $$$3(-4) \to 1(0) \to 2(-5) \to 2(-10) \to \ldots$$$
- $$$4(-3) \to 1(1) \to 3(-2) \to 4(-3) \to \ldots$$$
- $$$1(5) \to 3(2) \to 1(6) \to 2(1) \to 2(-4) \to \ldots$$$
- $$$1(9) \to 3(6) \to 2(1) \to 2(-4) \to \ldots$$$
| Название |
|---|




