| Codeforces Round 577 (Div. 2) |
|---|
| Закончено |
Вы находитесь на острове, который можно представить как таблицу $$$n \times m$$$. Строки таблицы пронумерованы целыми числами от $$$1$$$ до $$$n$$$, а столбцы пронумерованы целыми числами от $$$1$$$ до $$$m$$$. На острове расположено $$$k$$$ сокровищ, $$$i$$$-е из которых находится в клетке $$$(r_i, c_i)$$$.
Изначально вы находитесь в нижней левой клетке острова, в клетке $$$(1, 1)$$$. Если вы окажетесь в одной клетке с сокровищем, то вы можете забрать его, не тратя дополнительного времени. За один ход вы можете переместится вверх (из $$$(r, c)$$$ в $$$(r+1, c)$$$), налево (из $$$(r, c)$$$ в $$$(r, c-1)$$$) или направо (из $$$(r, c)$$$ в $$$(r, c+1)$$$). Из-за ловушек вы не можете двигаться вниз.
Однако двигаться вверх тоже небезопасно. Вы можете двигаться вверх, только если вы находитесь в безопасном столбце. Есть $$$q$$$ безопасных столбцов: $$$b_1, b_2, \ldots, b_q$$$. Вы хотите собрать все сокровища как можно быстрее. Выясните минимальное число ходов, за которое это можно сделать.
Первая строка содержит целые числа $$$n$$$, $$$m$$$, $$$k$$$ и $$$q$$$ ($$$2 \le n, \, m, \, k, \, q \le 2 \cdot 10^5$$$, $$$q \le m$$$) — количество строк, количество столбцов, количество сокровищ на острове и количество безопасных столбцов.
Каждая из $$$k$$$ следующих строк содержит целые числа $$$r_i, c_i$$$, ($$$1 \le r_i \le n$$$, $$$1 \le c_i \le m$$$) — координаты клеток, в которых расположены сокровища. Все сокровища расположены в различных клетках.
Последняя строка содержит $$$q$$$ различных чисел $$$b_1, b_2, \ldots, b_q$$$ ($$$1 \le b_i \le m$$$) — номера безопасных столбцов.
Выведите минимальное число ходов, которое нужно, чтобы собрать все сокровища.
3 3 3 2 1 1 2 1 3 1 2 3
6
3 5 3 2 1 2 2 3 3 1 1 5
8
3 6 3 2 1 6 2 2 3 4 1 6
15
В первом примере следует двигаться вверх во втором столбце, собирая в каждой строке сокровища, расположенные в первом столбце.
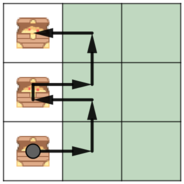
Во втором примере следует идти вверх в первом столбце.
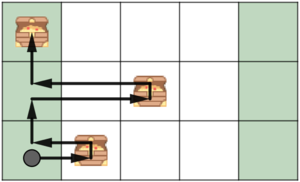
В третьем примере оптимально собрать сокровище в клетке $$$(1;6)$$$, затем переместиться вверх в строку $$$2$$$, используя столбец $$$6$$$, затем собрать сокровище в клетке $$$(2;2)$$$, подняться в верхний ряд, используя столбец $$$1$$$, и собрать последнее сокровище в клетке $$$(3;4)$$$. Всего $$$15$$$ ходов.

| Название |
|---|




