У вас есть строка $$$s$$$ — последовательность команд для робота. Робот находится в одной из клеток клетчатого поля. Он может выполнять следующие команды:
- 'W' — переместиться на одну клетку вверх;
- 'S' — переместиться на одну клетку вниз;
- 'A' — переместиться на одну клетку влево;
- 'D' — переместиться на одну клетку вправо.
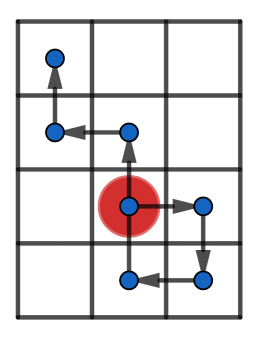
$$$Grid(s)$$$ — прямоугольное поле минимальной площади, такое, что на нем можно выбрать стартовую позицию робота так, что при выполнении всей последовательностей комнад $$$s$$$ робот не выйдет за пределы прямоугольника. Например, если $$$s = \text{DSAWWAW}$$$, то $$$Grid(s)$$$ — это прямоугольник $$$4 \times 3$$$.
- вы можете поместить робота в клетку $$$(3, 2)$$$;
- робот выполняет команду 'D' и перемещается в $$$(3, 3)$$$;
- робот выполняет команду 'S' и перемещается в $$$(4, 3)$$$;
- робот выполняет команду 'A' и перемещается в $$$(4, 2)$$$;
- робот выполняет команду 'W' и перемещается в $$$(3, 2)$$$;
- робот выполняет команду 'W' и перемещается в $$$(2, 2)$$$;
- робот выполняет команду 'A' и перемещается в $$$(2, 1)$$$;
- робот выполняет команду 'W' и перемещается в $$$(1, 1)$$$.
У вас есть $$$4$$$ дополнительных буквы: одна 'W', одна 'A', одна 'S' и одна 'D'. Вы можете вставить одну из них (либо не вставлять вообще) в любую позицию в строке $$$s$$$ для минимизации площади $$$Grid(s)$$$.
Какую минимальную площадь $$$Grid(s)$$$ вы можете получить?
Первая строка содержит число $$$T$$$ ($$$1 \le T \le 1000$$$) — количество запросов.
Следующие $$$T$$$ строк содержат запросы. Каждый запрос содержит строку $$$s$$$ ($$$1 \le |s| \le 2 \cdot 10^5$$$, $$$s_i \in \{\text{W}, \text{A}, \text{S}, \text{D}\}$$$) — последовательность команд.
Гарантируется, что суммарная длина строк $$$s$$$ по всем запросам не превосходит $$$2 \cdot 10^5$$$.
Выведите $$$T$$$ строк, по одному числу в каждой строке.
На каждый запрос выведите минимальное значение $$$Grid(s)$$$, которое вы можете получить.
3 DSAWWAW D WA
8 2 4
В первом запросе вам нужно получить строку $$$\text{DSAWW}\underline{D}\text{AW}$$$.
Во втором и третьем запросах вы не можете уменьшить площадь $$$Grid(s)$$$.
| Название |
|---|




