Вам дано $$$n$$$ массивов, которые могут иметь разные длины. Также вам дана таблица с $$$w$$$ столбцами и $$$n$$$ строками. $$$i$$$-й массив горизонтально расположен в $$$i$$$-й строке. Вы можете двигать каждый массив внутри его строки, но он должен всегда занимать подряд идущие клетки и лежать полностью внутри таблицы.
Вам нужно найти наибольшую возможную сумму чисел в $$$j$$$-м столбце для каждого $$$j$$$ от $$$1$$$ до $$$w$$$ независимо.
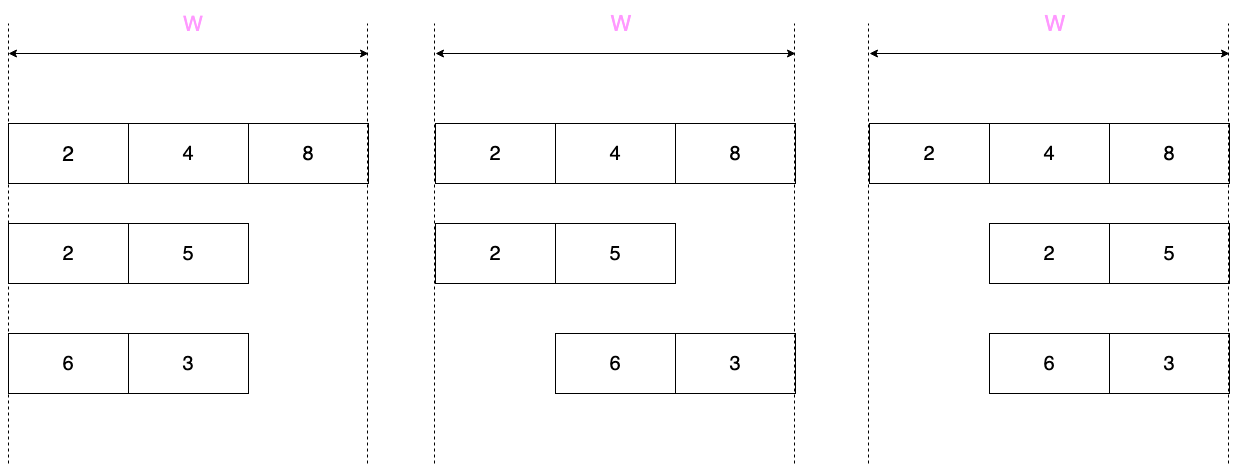 Оптимальные расположения для столбцов $$$1$$$, $$$2$$$ и $$$3$$$ изображены на изображениях слева направо.
Оптимальные расположения для столбцов $$$1$$$, $$$2$$$ и $$$3$$$ изображены на изображениях слева направо. Обратите внимание, что вы можете исключить любой массив из столбца (но только если он останется внутри своей строки). В таком случае значение полагается равным нулю.
В первой строке ввода записано два целых числа $$$n$$$ ($$$1 \le n \le 10^{6}$$$) и $$$w$$$ ($$$1 \le w \le 10^{6}$$$) — количество массивов и ширина таблицы.
Каждая из следующих $$$n$$$ строк содержит целое число $$$l_{i}$$$ ($$$1 \le l_{i} \le w$$$) — длина $$$i$$$-го массива, за которой следуют $$$l_{i}$$$ целых чисел $$$a_{i1}, a_{i2}, \ldots, a_{il_i}$$$ ($$$-10^{9} \le a_{ij} \le 10^{9}$$$) — элементы массива.
Суммарная длина массивов не превосходит $$$10^{6}$$$.
Выведите $$$w$$$ целых чисел, $$$i$$$-е из них должно равно максимальной сумме для столбца $$$i$$$.
3 3 3 2 4 8 2 2 5 2 6 3
10 15 16
2 2 2 7 8 1 -8
7 8
Изображения для первого примера находятся в условии.
| Название |
|---|




