Вам даны два целых числа $$$n$$$ и $$$k$$$.
Вам нужно построить $$$k$$$ правильных многоугольников с общей описанной окружностью с различными количествами сторон $$$l$$$ от $$$3$$$ до $$$n$$$.
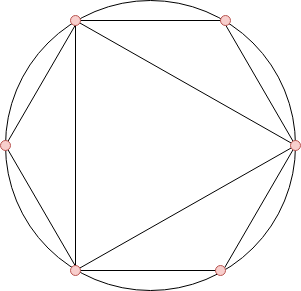Изображение к первому примеру. Вы можете вращать их, чтобы минимизировать количество различных точек на окружности. Найдите минимальное количество таких точек.
В первой строке ввода записаны два целых числа $$$n$$$ и $$$k$$$ ($$$3 \le n \le 10^{6}$$$, $$$1 \le k \le n-2$$$) — максимальное количество сторон у многоугольника и количество многоугольников, которое нужно построить, соответственно.
Выведите одно целое число — минимальное число точек на окружности, необходимых для размещения $$$k$$$ многоугольников.
6 2
6
200 50
708
В первом примере $$$n = 6$$$ и $$$k = 2$$$. Таким образом, есть $$$4$$$ многоугольника с количествами сторон $$$3$$$, $$$4$$$, $$$5$$$ и $$$6$$$ из которых нужно выбирать, и если выбрать треугольник и шестиугольник, получится картинка из условия.
Таким образом, минимальное необходимое количество точек на круге $$$6$$$, что также минимально по всем возможных множествам.
