Вам дано дерево с $$$n$$$ вершинами. Дерево подвешено за вершину $$$1$$$, которая не считается листом не зависимо от ее степени.
Каждый лист покрашен в один из двух цветов: красный или синий. Листовая вершина с номером $$$v$$$ исходно имеет цвет $$$s_{v}$$$.
Цвет каждой из внутренней вершины (включая корень) определятся следующим образом.
- Обозначим за $$$b$$$ количество синих непосредственных детей, и за $$$r$$$ количество красных непосредственных детей данной вершины.
- Тогда цвет этой вершины синий тогда и только тогда, когда $$$b - r \ge k$$$, иначе он красный.
Число $$$k$$$ это параметр, одинаковый для всех вершин.
Вам необходимо обработать запросы следующих типов:
- 1 v: вывести цвет вершины $$$v$$$;
- 2 v c: изменить цвет листа $$$v$$$ на $$$c$$$ ($$$c = 0$$$ означает красный, $$$c = 1$$$ означает синий);
- 3 h: изменить текущее значение $$$k$$$ на $$$h$$$.
Первая строка ввода содержит два целых числа $$$n$$$ и $$$k$$$ ($$$2 \le n \le 10^{5}$$$, $$$-n \le k \le n$$$) — количество вершин и исходное значение $$$k$$$.
Каждая из следующих $$$n - 1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), описывающих, что есть ребро, соединяющее вершины $$$u$$$ и $$$v$$$.
Следующая строка состоит из $$$n$$$ целых чисел, разделенных пробелами — исходный массив $$$s$$$ ($$$-1 \le s_i \le 1$$$). $$$s_{i} = 0$$$ означает, что цвет вершины $$$i$$$ красный. $$$s_{i} = 1$$$ означает, что цвет вершины $$$i$$$ синий. $$$s_{i} = -1$$$ означает, что вершина $$$i$$$ не является листом.
Следующая строка содержит целое число $$$q$$$ ($$$1 \le q \le 10^5$$$), количество запросов.
Затем следуют $$$q$$$ строк, каждая содержит запрос, который необходимо обработать:
- 1 v ($$$1 \le v \le n$$$): вывести цвет вершины $$$v$$$;
- 2 v c ($$$1 \le v \le n$$$, $$$c = 0$$$ or $$$c = 1$$$): изменить цвет листа $$$v$$$ на $$$c$$$ ($$$c = 0$$$ означает красный, $$$c = 1$$$ означает синий). Гарантируется, что $$$v$$$ это лист;
- 3 h ($$$-n \le h \le n$$$): изменить текущее значение $$$k$$$ на $$$h$$$.
Для каждого запроса первого типа выведите $$$0$$$, если цвет вершины $$$v$$$ красный, и $$$1$$$ иначе.
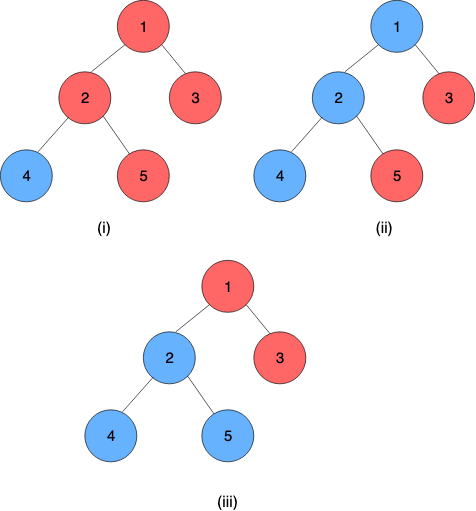
5 2 1 2 1 3 2 4 2 5 -1 -1 0 1 0 9 1 1 1 2 3 -2 1 1 1 2 3 1 2 5 1 1 1 1 2
0 0 1 1 0 1
(i) Исходное дерево
(ii) Дерево после 3-го запроса
(iii) Дерево после 7-го запроса
| Название |
|---|




