Камил любит стримить видео по спортивному программированию. Его канал на MeTube недавно набрал $$$100$$$ миллионов подписчиков. Чтобы отпраздновать это, он выложил видео с интересной задачей, которую он пока не может решить. Можете ли вы помочь ему?
Вам дано дерево — связный неориентированный граф состоящий из $$$n$$$ вершин и $$$n - 1$$$ ребер. Дерево подвешено за вершину $$$1$$$. Вершина $$$u$$$ является предком $$$v$$$ если она лежит на кратчайшем пути между корнем и $$$v$$$. В частности, вершина является предком себя.
У каждой вершины $$$v$$$ есть красота $$$x_v$$$ — неотрицательное целое число не большее $$$10^{12}$$$. Это позволяет нам определить красоту пути. Пусть $$$u$$$ предок $$$v$$$. Тогда определим красоту $$$f(u, v)$$$ как наибольший общий делитель красот всех вершин на кратчайшем пути между $$$u$$$ и $$$v$$$. Формально, если $$$u=t_1, t_2, t_3, \dots, t_k=v$$$ — вершины на кратчайшем пути между $$$u$$$ и $$$v$$$, тогда $$$f(u, v) = \gcd(x_{t_1}, x_{t_2}, \dots, x_{t_k})$$$. Тут $$$\gcd$$$ обозначает наибольший общий делитель множества чисел. В частности, $$$f(u, u) = \gcd(x_u) = x_u$$$.
Ваша задача найти сумму
$$$$$$ \sum_{u\text{ предок }v} f(u, v). $$$$$$
Так как ответ может быть слишком большим, выведите его по модулю $$$10^9 + 7$$$.
Обратите внимание что для любого $$$y$$$, $$$\gcd(0, y) = \gcd(y, 0) = y$$$. В частности, $$$\gcd(0, 0) = 0$$$.
В первой строке записано одно целое число $$$n$$$ ($$$2 \le n \le 100\,000$$$) — количество вершин в дереве.
В следующей строке записаны $$$n$$$ целых чисел $$$x_1, x_2, \dots, x_n$$$ ($$$0 \le x_i \le 10^{12}$$$). Значение $$$x_v$$$ обозначает красоту вершины $$$v$$$.
В следующих $$$n - 1$$$ строках описаны ребра дерева. Каждая из них содержит два целых числа $$$a, b$$$ ($$$1 \le a, b \le n$$$, $$$a \neq b$$$) — вершины соединенные ребром.
Выведите сумму красот всех таких путей $$$(u, v)$$$, что $$$u$$$ предок $$$v$$$. Эта сумма должна быть выведена по модулю $$$10^9 + 7$$$.
5 4 5 6 0 8 1 2 1 3 1 4 4 5
42
7 0 2 3 0 0 0 0 1 2 1 3 2 4 2 5 3 6 3 7
30
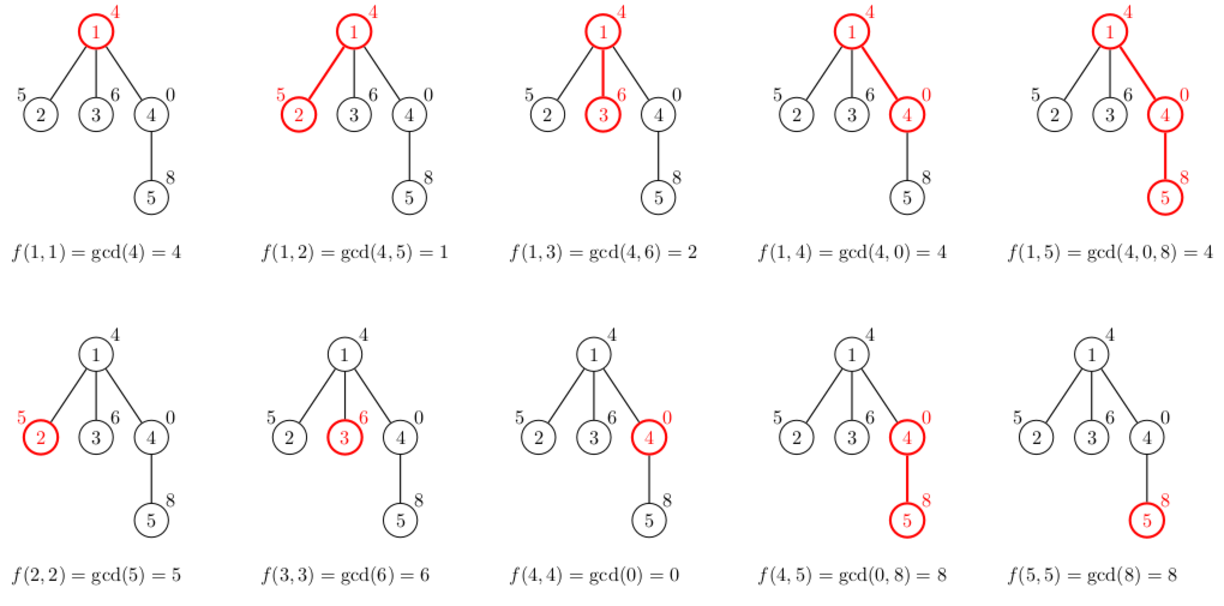
На следующей иллюстрации изображены все $$$10$$$ возможных путей, в которых один из концов является предком другого. Сумма красот всех этих путей равна $$$42$$$:
| Название |
|---|




