| Kotlin Heroes: Episode 2 |
|---|
| Закончено |
- Kotlin 1.7.20
- Kotlin 1.9.21
В Древляндии $$$n$$$ городов и $$$n-1$$$ двусторонняя дорога. Каждая дорога соединяет пару различных городов. Из любого города можно проехать в любой другой, двигаясь только по дорогам. Города пронумерованы от $$$1$$$ до $$$n$$$. Да, конечно, вы узнали в этом описании неориентированное дерево.
В каждом городе хранится один флаг, цвет флага в $$$i$$$-м городе равен $$$c_i$$$. Возможно, что цвета флагов в разных городах совпадают.
Если король едет по маршруту $$$[u_1, u_2, u_3, \dots, u_k]$$$, то это значит, что он стартует в городе $$$u_1$$$, затем перемещается в город $$$u_2$$$ ($$$u_2$$$ соединён дорогой с $$$u_1$$$), затем из $$$u_2$$$ в $$$u_3$$$ ($$$u_3$$$ соединён дорогой с $$$u_2$$$), и так далее пока не приедет в город $$$u_k$$$. Возможно, что в процессе такого маршрута король посетит один и тот же город более одного раза. Иными словами, маршрут $$$[u_1, u_2, u_3, \dots, u_k]$$$ не обязательно состоит только из различных городов. В терминах теории графов — король перемещается из $$$u_1$$$ в $$$u_k$$$ по некоторому пути $$$[u_1, u_2, u_3, \dots, u_k]$$$, который не обязательно является простым (для всех $$$j$$$ от $$$1$$$ до $$$k-1$$$ города $$$u_j$$$ и $$$u_{j+1}$$$ соединены дорогой).
Когда король перемещается из одного города в другой, то главы городов в знак своей дружбы обмениваются флагами.
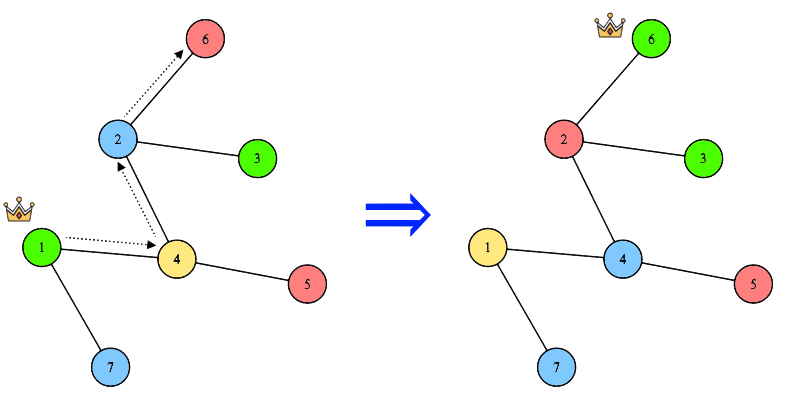 Пример перемещения короля по маршруту $$$[1, 4, 2, 6]$$$. Цвет вершины соответствуют цвету флага в этой вершине.
Пример перемещения короля по маршруту $$$[1, 4, 2, 6]$$$. Цвет вершины соответствуют цвету флага в этой вершине. Из эстетических соображений, король хочет, чтобы цвет флага в городе $$$i$$$ был равен $$$d_i$$$ для всех $$$i$$$ от $$$1$$$ до $$$n$$$. Определите, может ли король выбрать какой-то маршрут и проехать по нему так, чтобы для каждого города цвет флага в нём оказался равен желаемому цвету $$$d_i$$$. Обратите внимание, что король может выбрать (и проехать) ровно один маршрут. В случае положительного ответа, найдите кратчайший возможный маршрут короля.
В случае, если начальные цвета флагов уже соответствуют требованиям короля (то есть $$$c_i=d_i$$$ для всех $$$i$$$), то считайте, что король совершает маршрут длины $$$k=0$$$.
В первой строке задано целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных в тесте. Далее следуют наборы входных данных.
Каждый набор входных данных начинается строкой, содержащей целое число $$$n$$$ ($$$2 \le n \le 2\cdot10^5$$$) — количество городов Древляндии.
Далее следует строка из $$$n$$$ целых чисел $$$c_1, c_2, \dots, c_n$$$ ($$$1 \le c_i \le 10^6$$$), где $$$c_i$$$ обозначает цвет флага в $$$i$$$-й вершине до старта перемещения короля.
Далее следует строка из $$$n$$$ целых чисел $$$d_1, d_2, \dots, d_n$$$ ($$$1 \le d_i \le 10^6$$$), где $$$d_i$$$ обозначает требуемый цвет флага в $$$i$$$-й вершине после завершения перемещения короля.
Далее в $$$n-1$$$ строке перечислены дороги Древляндии. Каждая дорога задана строкой, содержащей два целых числа $$$x_j, y_j$$$ ($$$1 \le x_j, y_j \le n$$$) — номера городов, которые соединены $$$j$$$-й дорогой.
Гарантируется, что из каждого города можно добраться в любой другой по дорогам (иными словами, система городов и дорог образует неориентированное дерево).
Сумма всех значений $$$n$$$ по всем наборам входных данных в одном тесте не превосходит $$$2\cdot10^5$$$.
Выведите ответы на все наборы в порядке их следования во входных данных.
Каждый ответ должен начинаться со строки, содержащей «Yes» (в случае положительного ответа) или «No» (в случае, если искомого маршрута не существует). В случае положительного ответа следующая строка должна содержать целое число $$$k$$$ — количество городов в кратчайшем возможном маршруте короля. Следующая строка должна содержать сам искомый маршрут $$$u_1, u_2, \dots, u_k$$$ ($$$1 \le u_i \le n$$$). Вы можете не выводить эту строку, если $$$k=0$$$.
1 7 2 3 2 7 1 1 3 7 1 2 3 1 2 3 1 7 4 1 2 6 2 3 2 4 5 4
Yes 4 1 4 2 6
1 5 1 2 2 2 2 2 2 2 2 1 1 2 2 3 3 4 4 5
Yes 5 1 2 3 4 5
3 4 10 20 10 20 20 10 20 10 1 2 1 3 1 4 2 1000000 1000000 1000000 1000000 1 2 10 4 2 2 4 2 4 1 2 3 4 4 2 4 4 3 2 1 2 4 2 5 8 6 9 10 5 1 10 7 10 3 4 5 9 3 10 2 4
No Yes 0 Yes 5 3 10 5 9 6
| Название |
|---|




