Недавно у Пети был день рождения. Его друзья знают, что Петя очень сильно любит головоломки, поэтому они подарили ему популярный конструктор «Электрик-$$$n$$$».
Конструктор «Электрик-$$$n$$$» состоит из $$$2n - 1$$$ проводов и $$$2n$$$ лампочек. При этом каждая лампочка имеет свой уникальный номер, являющийся целыми числом от $$$1$$$ до $$$2n$$$, а все провода являются одинаковыми и неразличимы. Чтобы собрать конструктор требуется каждый из проводов использовать для соединения каких-то двух различных лампочек. Цепочкой в собранном конструкторе назовём последовательность из не менее чем двух различных лампочек, такую что любые две соседние в цепочке лампочки соединены проводом напрямую. Итоговая конфигурация конструктора является корректной, если сеть из проводов и лампочек имеет древовидную структуру, то есть любые две различные лампочки являются концами какой-нибудь цепочки.
На протяжении нескольких дней Петя собирал различные конфигурации. Он обратил внимание на то, что иногда некоторые лампочки начинают светиться. После продолжительных экспериментов Петя выяснил, что лампочки с номерами $$$2i$$$ и $$$2i - 1$$$ горят тогда, когда цепочка между ними состоит ровно из $$$d_i$$$ проводов. При этом выполнялось важное условие: значение $$$d_i$$$ всегда было не больше $$$n$$$.
Сколько бы Петя не старался, у него так и не получилось найти конфигурацию, в которой бы светились все лампочки, поэтому он решил попросить помощи у вас. Требуется найти любую корректную конфигурацию, в которой горят все лампочки. Гарантируется, что это всегда возможно сделать.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \leq n \leq 100\,000$$$) — параметр конструктора, определяющий количество лампочек и количество проводов.
В следующей строке записаны $$$n$$$ целых чисел $$$d_1, d_2, \ldots, d_n$$$ ($$$1 \leq d_i \leq n$$$), где $$$d_i$$$ — требуемое число проводов в цепочке, чтобы лампочки $$$2i$$$ и $$$2i - 1$$$ светились.
Выведите $$$2n - 1$$$ строк. В $$$i$$$-й строке должны быть записаны два различных целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \leq a_i, b_i \leq 2n$$$, $$$a_i \ne b_i$$$), которые означают, что в вашей конфигурации лампочки с этими номерами соединены проводом.
Если существует несколько правильных ответов, то разрешается вывести любой из них.
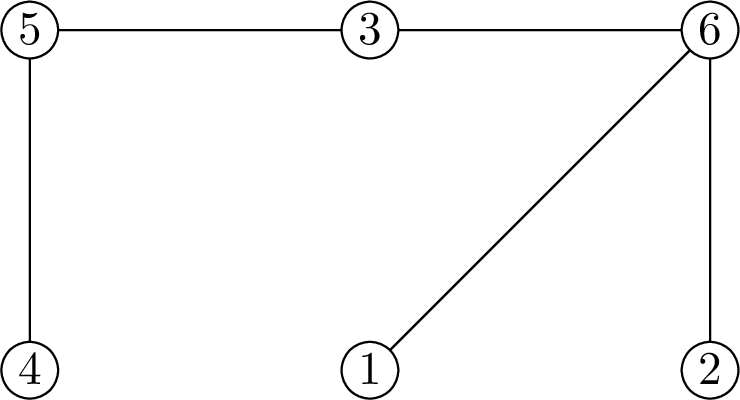
3 2 2 2
1 6 2 6 3 5 3 6 4 5
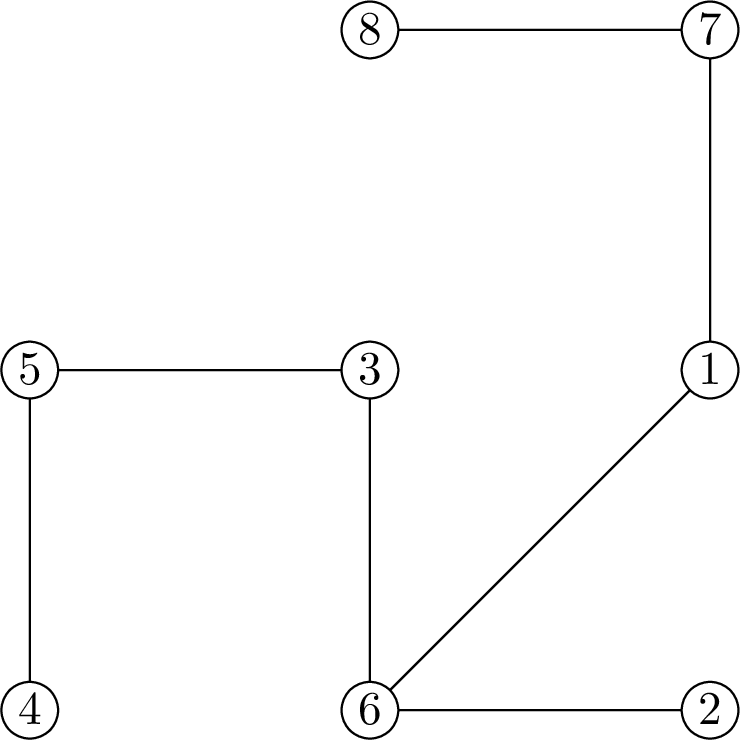
4 2 2 2 1
1 6 1 7 2 6 3 5 3 6 4 5 7 8
6 2 2 2 2 2 2
1 3 2 3 3 5 4 5 5 7 6 7 7 12 8 12 9 11 9 12 10 11
2 1 1
1 2 1 4 3 4
| Название |
|---|




