| Codeforces Round 586 (Div. 1 + Div. 2) |
|---|
| Закончено |
Садовод Леша очень любит выращивать деревья. Напомним, что деревом называется связный ациклический граф на $$$n$$$ вершинах.
Сегодня он решил вырастить подвешенное бинарное дерево. Бинарным деревом называется дерево, в котором у каждой вершины не больше двух сыновей. К счастью, у Леши еще с прошлого дня рождения завалялась перестановка чисел от $$$1$$$ до $$$n$$$, поэтому он решил вырастить дерево по этой перестановке. Для этого он совершает следующий процесс: находит минимум в перестановке, создает соответствующую ему вершину и делает ее корнем дерева. После этого перестановка разделяется на две части: все, что левее минимального элемента, и все, что правее. Минимумы на левой и правой части становятся левыми и правыми сыновьями корня соответственно, после чего на левой и правой части производится рекурсивно тот же процесс.
Теперь Леша хочет вырастить целый лес деревьев: по одному дереву на каждый циклический сдвиг перестановки. Ему интересно, при каком циклическом сдвиге глубина полученного дерева будет минимальной. Но, к сожалению, выращивание леса — дело долгое, а ответ интересен Леше прямо сейчас. Поможете ему?
Напомним, что циклическим сдвигом перестановки $$$a_1, a_2, \ldots, a_k, \ldots, a_n$$$ на $$$k$$$ элементов влево называется перестановка $$$a_{k + 1}, a_{k + 2}, \ldots, a_n, a_1, a_2, \ldots, a_k$$$.
Первая строка содержит целое число $$$n ~ (1 \leqslant n \leqslant 200\,000)$$$ — длина перестановки.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n ~ (1 \leqslant a_i \leqslant n)$$$, при этом гарантируется, что каждое число встречается ровно один раз.
Через пробел выведите два числа: минимальная глубина дерева, которую можно получить, и на сколько нужно циклически сдвинуть перестановку влево, чтобы получить дерево минимальной глубины. Величина сдвига должна быть числом от $$$0$$$ до $$$n - 1$$$. Если возможных ответов несколько, выведите любой.
4 1 2 3 4
3 3
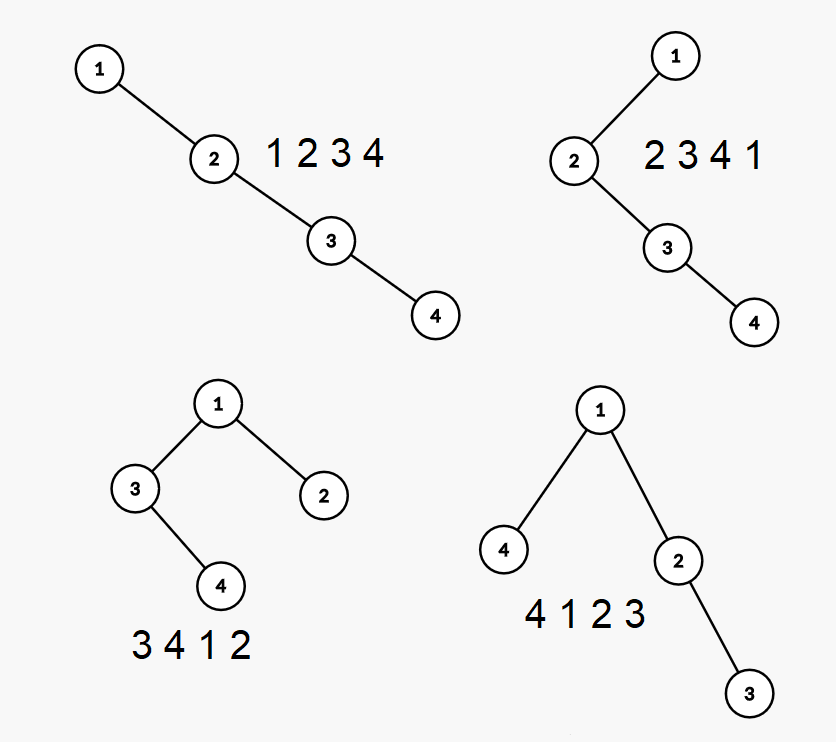
На картинке ниже изображены все возможные деревья для перестановки из примера, а рядом с ними написаны циклические сдвиги, из которых они получаются.
| Название |
|---|




