Недавно Петя нашел игру «Выбери квадрат». В игре на бесконечном поле расположено $$$n$$$ точек, пронумерованных целыми числами от $$$1$$$ до $$$n$$$. Точка номер $$$i$$$ имеет координаты $$$(x_i, y_i)$$$ и стоимость $$$c_i$$$.
Необходимо выбрать квадрат, стороны которого параллельны осям координат, левый нижний и правый верхний угол лежат на прямой $$$y = x$$$, и все углы имеют целые координаты.
Счетом игры является разность суммарной стоимости точек, покрытых выбранным квадратом, и длины стороны квадрата. Сторона квадрата может быть нулевой длины.
Петя просит вас помочь ему найти максимальный счет в игре, выбрав ровно один квадрат.
Первая строка входных данных содержит одно целое число $$$n$$$ ($$$1 \le n \le 5 \cdot 10^5$$$) — количество точек на поле.
Каждая из следующих $$$n$$$ строк содержит три целых числа $$$x_i, y_i, c_i$$$ ($$$0 \le x_i, y_i \le 10^9, -10^6 \le c_i \le 10^6$$$) — координаты $$$i$$$-й точки и ее стоимость, соответственно.
В первой строке выведите максимальный счет, который можно набрать в игре, выбрав ровно один квадрат.
Во второй строке выведите четыре целых числа $$$x_1, y_1, x_2, y_2$$$ ($$$0 \le x_1, y_1, x_2, y_2 \le 2 \cdot 10^9, x_1 = y_1, x_2 = y_2, x_1 \le x_2$$$), разделенные пробелами — координаты левого нижнего и правого верхнего углов квадрата, которые необходимо выбрать Пете, чтобы набрать максимальный счет.
6 0 0 2 1 0 -5 1 1 3 2 3 4 1 4 -4 3 1 -1
4 1 1 3 3
5 3 3 0 3 3 -3 0 2 -1 3 1 3 0 0 -2
0 1 1 1 1
Игровое поле, соответствующее первому тестовому примеру: 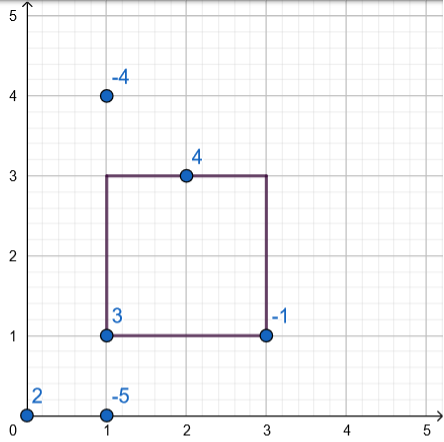
| Название |
|---|




