| Технокубок 2020 - Отборочный Раунд 1 |
|---|
| Закончено |
Вам задано взвешенное дерево, состоящее из $$$n$$$ вершин. Напомним, что деревом называется связный граф без циклов. Вершины $$$u_i$$$ и $$$v_i$$$ соединены ребром веса $$$w_i$$$.
Определим $$$k$$$-раскраску дерева как присвоение каждой вершине ровно $$$k$$$ цветов, таким образом, что каждый цвет используется не более двух раз. Считайте, что различных доступных цветов бесконечно много. Назовем ребро насыщенным в $$$k$$$-раскраске, если его концы имеют хотя бы один общий цвет (т.е. найдется цвет, который присвоен обоим концам ребра).
Так же определим счет $$$k$$$-раскраски как сумму весов насыщенных ребер.
Вам необходимо найти максимально возможный счет $$$k$$$-раскраски заданного дерева.
Вам нужно ответить на $$$q$$$ независимых запросов.
Первая строка содержит целое число $$$q$$$ ($$$1 \le q \le 5 \cdot 10^5$$$) — количество запросов.
Первая строка каждого запроса содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n, k \le 5 \cdot 10^5$$$) — количество вершин в дереве и количество цветов, которое нужно присвоить каждой вершине.
Каждая из следующих $$$n - 1$$$ строк описывает ребра дерева. Ребро $$$i$$$ обозначается тремя целыми числами $$$u_i$$$, $$$v_i$$$ и $$$w_i$$$ — номерами вершин, которые оно соединяет, и весом ребра ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$, $$$1 \le w_i \le 10^5$$$). Гарантируется, что заданный набор ребер образует дерево.
Гарантируется, что сумма $$$n$$$ по всем запросам не превосходит $$$5 \cdot 10^5$$$.
На каждый запрос выведите одно целое число — максимально возможный счет $$$k$$$-раскраски заданного дерева.
2 4 1 1 2 5 3 1 2 3 4 3 7 2 1 2 5 1 3 4 1 4 2 2 5 1 2 6 2 4 7 3
8 14
Дерево, соответствующее первому запросу в тестовом примере:
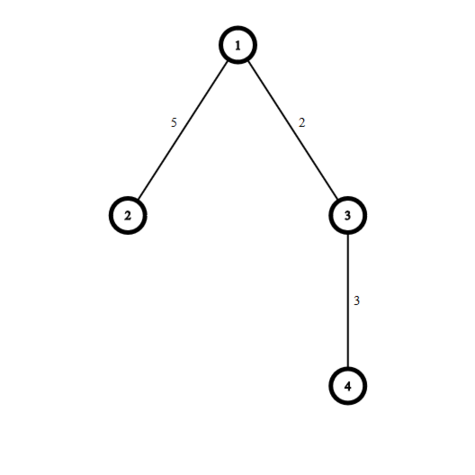
Одна из возможных $$$k$$$-раскрасок в первом запросе: $$$(1), (1), (2), (2)$$$, тогда ребра номер $$$1$$$ и $$$3$$$ являются насыщенными и сумма их весов равна $$$8$$$.
Дерево, соответствующее второму запросу в тестовом примере:
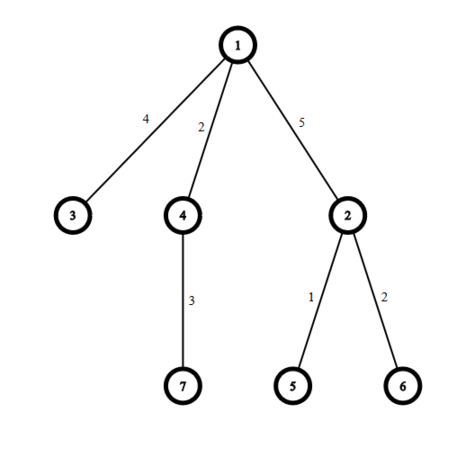
Одна из возможных $$$k$$$-раскрасок во втором запросе: $$$(1, 2), (1, 3), (2, 4), (5, 6), (7, 8), (3, 4), (5, 6)$$$, тогда ребра номер $$$1$$$, $$$2$$$, $$$5$$$ и $$$6$$$ являются насыщенными и сумма их весов равна $$$14$$$.
| Название |
|---|




