| Codeforces Round 589 (Div. 2) |
|---|
| Закончено |
Дан неориентированный простой граф, который состоит из $$$n$$$ вершин и $$$m$$$ ребер. Граф не содержит петель (то есть каждое ребро соединяет две различные вершины), между каждой парой вершин существует не более одного ребра. Заданный граф может быть несвязным.
Определим следующее:
Пусть $$$v_1$$$ и $$$v_2$$$ два некоторых непустых подмножества вершин, которые не пересекаются. Пусть $$$f(v_{1}, v_{2})$$$ будет истиной (true) тогда и только тогда, когда все условия удовлетворены:
- Нет ребра, которые соединяет две вершины в множестве вершин $$$v_1$$$.
- Нет ребра, которые соединяет две вершины в множестве вершин $$$v_2$$$.
- Для каждых двух вершин $$$x$$$ и $$$y$$$ таких, что $$$x$$$ находится в $$$v_1$$$ и $$$y$$$ находится в $$$v_2$$$, есть ребро, которое соединяет $$$x$$$ и $$$y$$$.
Создайте три множества вершин ($$$v_{1}$$$, $$$v_{2}$$$, $$$v_{3}$$$) таких, что все условия удовлетворены;
- Все множества не должны быть пустыми.
- Каждая вершина должна принадлежать ровно одному множеству.
- $$$f(v_{1}, v_{2})$$$, $$$f(v_{2}, v_{3})$$$, $$$f(v_{3}, v_{1})$$$ должны быть истинами (true).
Возможно ли создать такие три множества? Есть это так, выведите такое разбиение вершин.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$3 \le n \le 10^{5}$$$, $$$0 \le m \le \text{min}(3 \cdot 10^{5}, \frac{n(n-1)}{2})$$$) — количество вершин и ребер в графе.
$$$i$$$-я из следующих $$$m$$$ строк содержит два целых числа $$$a_{i}$$$ и $$$b_{i}$$$ ($$$1 \le a_{i} \lt b_{i} \le n$$$), которые значат, что существует ребро между $$$a_{i}$$$ и $$$b_{i}$$$. Граф не содержит петель (то есть каждое ребро соединяет две различные вершины), между каждой парой вершин существует не более одного ребра. Заданный граф может быть несвязным.
Если ответ существует, выведите $$$n$$$ целых чисел. $$$i$$$-е целое число обозначает номер множества (от $$$1$$$ до $$$3$$$), к которому принадлежит $$$i$$$-я вершина. Иначе выведите $$$-1$$$.
Если существует несколько решений, выведите любое из них.
6 11 1 2 1 3 1 4 1 5 1 6 2 4 2 5 2 6 3 4 3 5 3 6
1 2 2 3 3 3
4 6 1 2 1 3 1 4 2 3 2 4 3 4
-1
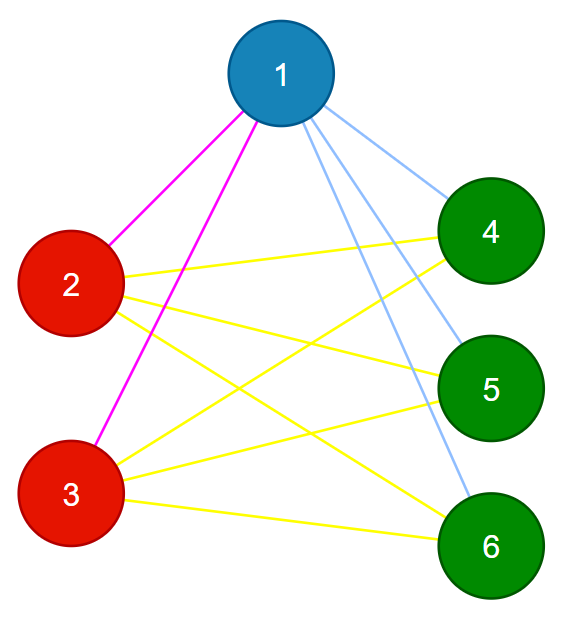
В первом примере, если $$$v_{1} = \{ 1 \}$$$, $$$v_{2} = \{ 2, 3 \}$$$ и $$$v_{3} = \{ 4, 5, 6 \}$$$, тогда множества будут удовлетворять всем условиям. Но также существует и другое разбиение. Например, «2 3 3 1 1 1», который также будет засчитан как правильный ответ.
Во втором примере правильное разбиение не существует.
| Название |
|---|




