| Codeforces Round 589 (Div. 2) |
|---|
| Закончено |
Дано целое число $$$n$$$. Определим следующее дерево деревом McDic:
- Создадим полное бинарное дерево с $$$2^{n} - 1$$$ вершинами. То есть дерево, где ровно одна вершина является корнем, все листы имеют одинаковую высоту (расстояние до корня) и все не листовые вершины имеют по два прямых потомка.
- Выберем любую некорневую вершину $$$v$$$ из этого бинарного дерева.
- Удалим $$$v$$$ из дерева и проведем ребра между предком $$$v$$$ и прямыми потомками $$$v$$$. Если у $$$v$$$ нет потомков, тогда ребра не добавляются.
Дано дерево. Определите, является ли это дерево деревом McDic. Если да, найдите предка удаленной вершины.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 17$$$).
$$$i$$$-я из следующих $$$2^{n} - 3$$$ строк содержит два целых числа $$$a_{i}$$$ и $$$b_{i}$$$ ($$$1 \le a_{i} \lt b_{i} \le 2^{n} - 2$$$), которые значат, что существует ребро между $$$a_{i}$$$ и $$$b_{i}$$$. Гарантируется, что граф — дерево.
Выведите две строки.
В первой строке выведите одно целое число — количество ответов. Если это дерево не является деревом McDic, то выведите $$$0$$$.
Во второй строке выведите все возможные ответы в возрастающем порядке. Если это дерево не является деревом McDic, то ничего не выводите.
4 1 2 1 3 2 4 2 5 3 6 3 13 3 14 4 7 4 8 5 9 5 10 6 11 6 12
1 3
2 1 2
2 1 2
3 1 2 2 3 3 4 4 5 5 6
0
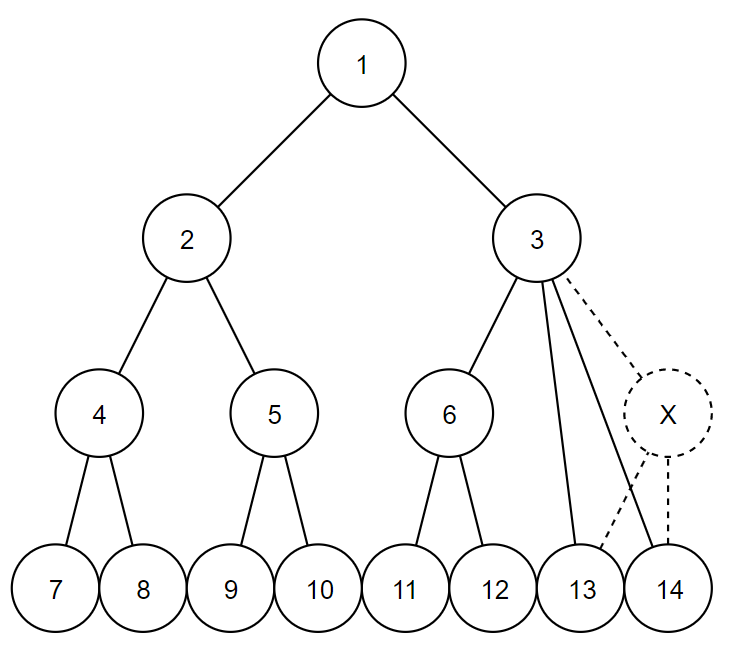
В первом примере $$$3$$$ — это единственный возможный ответ.
Во втором примере есть $$$2$$$ возможных ответа.

В третьем примере дерево не является деревом McDic.
| Название |
|---|




