| Codeforces Global Round 5 |
|---|
| Закончено |
Напомним, что двоичным деревом поиска называется корневое дерево, каждая вершина которого хранит ключ и может иметь не более двух поддеревьев — левого и правого. Ключ в каждой вершине должен быть больше любого ключа в левом поддереве и меньше любого ключа в правом поддереве.
Глубина вершины определяется как число рёбер на простом пути между вершиной и корнем дерева. В частности, глубина корня равна $$$0$$$.
Будем называть двоичное дерево поиска идеально сбалансированным, если не существует двоичного дерева поиска с тем же числом вершин, у которого суммарная глубина всех вершин строго меньше.
Будем называть двоичное дерево поиска с целочисленными ключами полосатым, если для каждой вершины $$$v$$$ выполняются оба следующих условия:
- Если у $$$v$$$ есть левое поддерево с корнем в $$$u$$$, чётность ключа $$$v$$$ должна отличаться от чётности ключа $$$u$$$.
- Если у $$$v$$$ есть правое поддерево с корнем в $$$w$$$, чётность ключа $$$v$$$ должна совпадать с чётностью ключа $$$w$$$.
Вам дано целое число $$$n$$$. Найдите число идеально сбалансированных полосатых двоичных деревьев поиска из $$$n$$$ вершин, ключи которых — различные целые числа от $$$1$$$ до $$$n$$$ включительно. Выведите остаток от деления этого числа на $$$998\,244\,353$$$.
Единственная строка содержит целое число $$$n$$$ ($$$1 \le n \le 10^6$$$) — требуемое число вершин в дереве.
Выведите число идеально сбалансированных полосатых двоичных деревьев поиска из $$$n$$$ вершин, ключи которых — различные целые числа от $$$1$$$ до $$$n$$$ включительно, по модулю $$$998\,244\,353$$$.
4
1
3
0
В первом примере единственное дерево, удовлетворяющее условиям, выглядит так: 
А так выглядят деревья, не удовлетворяющие различным условиям во втором примере: 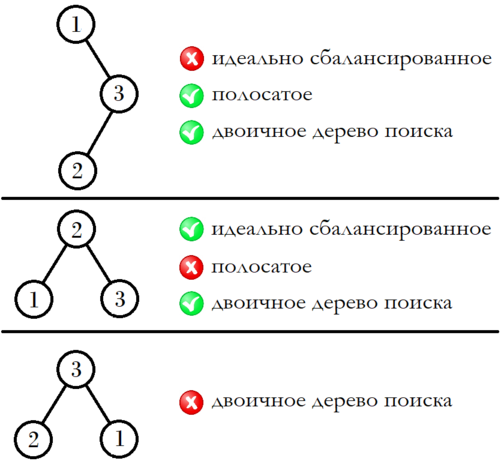
| Название |
|---|




