Пусть у вас есть $$$k$$$ одномерных отрезков $$$s_1, s_2, \dots s_k$$$ (каждый отрезок представляется двумя числами — координатами его концов). Тогда вы можете построить граф из $$$k$$$ вершин на этих отрезках. Между $$$i$$$-й и $$$j$$$-й вершинами ($$$i \neq j$$$) есть ребро тогда и только тогда, когда отрезки $$$s_i$$$ и $$$s_j$$$ пересекаются (когда существует хотя бы одна точка, принадлежащая обоим отрезкам).
Например, если $$$s_1 = [1, 6], s_2 = [8, 20], s_3 = [4, 10], s_4 = [2, 13], s_5 = [17, 18]$$$, то граф будет выглядеть следующим образом:
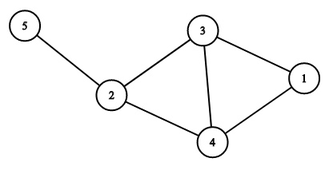
Дерево размера $$$m$$$ считается хорошим, если можно выбрать $$$m$$$ таких одномерных отрезков, что граф, построенный на этих отрезках, совпадает с деревом.
Вам задано дерево, найдите максимальный размер хорошего поддерева этого дерева. Напомним, что поддеревом называется связный подграф дерева.
Обратите внимание, что вам нужно ответить на $$$q$$$ независимых запросов.
Первая строка содержит число $$$q$$$ ($$$1 \le q \le 15 \cdot 10^4$$$) — количество запросов.
Первая строка каждого запроса содержит число $$$n$$$ ($$$2 \le n \le 3 \cdot 10^5$$$) — количество вершин дерева.
Каждая из следующих $$$n - 1$$$ содержит два числа $$$x$$$ и $$$y$$$ ($$$1 \le x, y \le n$$$) — ребро между вершинами $$$x$$$ и $$$y$$$. Гарантируется, что заданный граф является деревом.
Гарантируется, что сумма всех $$$n$$$ не превосходит $$$3 \cdot 10^5$$$.
На каждый запрос выведите одно число — максимальный размер хорошего поддерева заданного дерева.
1 10 1 2 1 3 1 4 2 5 2 6 3 7 3 8 4 9 4 10
8
В первом запросе одно из хороших поддеревьев размера $$$8$$$ состоит из вершин: $$${9, 4, 10, 2, 5, 1, 6, 3}$$$.
| Название |
|---|




