| Codeforces Round 594 (Div. 1) |
|---|
| Закончено |
В ожидании новых приключений Башмачок захотел совершить доброе дело. Посовещавшись с Картой и Рюкзаком, он решил подарить Даше связный граф. После долгих поисков, Башмачок выбрал $$$t$$$ вариантов графа, которые могли бы понравиться Даше, но, к сожалению, все его планы решил испортить лис Жулик.
Жулик знает, что Даша пока умеет считать только до $$$3$$$, поэтому у него родилась идея. Он хочет украсть непустой набор вершин так, чтобы Даша не заметила пропажи. Поэтому он решил украсть непустой набор вершин такой, что если удалить выбранные вершины и связанные с ними рёбра из графа, то для любой из оставшихся вершин будет верно, что её степень (число смежных рёбер) будет иметь такой же остаток от деления на $$$3$$$, что и степень до удаления рёбер. Также он понял, что будет слишком подозрительно, если он украдёт все вершины, поэтому он решил воздержаться от такой соблазнительной затеи.
Башмачок понял, что он не может позволить случиться преступлению. Но он боится, что одному ему не справиться. Поэтому он решил попросить у вас помощи. Башмачок хочет для каждого варианта графа узнать, сможет ли Жулик осуществить свои злобные планы, или нет.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 100\,000$$$) — количество вариантов графа.
Первая строка описания каждого варианта содержит целые числа $$$n$$$, $$$m$$$ ($$$1 \le n \le 500\,000$$$, $$$0 \le m \le 500\,000$$$) — количество вершин и рёбер в графе.
Затем следуют $$$m$$$ строк, в каждой из которых записаны целые числа $$$a_i$$$, $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$) — номера вершин, соединённых очередным ребром.
Гарантируется, что граф связен и что в нём нет кратных рёбер и петель.
Гарантируется, что сумма $$$n$$$ по всем вариантам не превосходит $$$500\,000$$$, и что сумма $$$m$$$ по всем вариантам не превосходит $$$500\,000$$$.
Описания вариантов графа разделены одной пустой строкой.
Для каждого варианта:
- В случае, если ответ существует, выведите «Yes», а затем сам пример.
Первая строка примера должна содержать целое число $$$c$$$ ($$$1 < c < n$$$) — количество вершин, которые может украсть Жулик, чтобы Даша не заметила пропажи. В следующей строке выведите $$$c$$$ различных чисел — номера этих вершин в произвольном порядке.
- Иначе выведите «No».
Если существует несколько способов украсть вершины требуемым образом, выведите любой из них.
Обратите внимание, что необязательно красть максимальное возможное число вершин.
3 3 3 1 2 2 3 3 1 6 6 1 2 1 3 2 3 2 5 2 6 2 4 8 12 1 2 1 3 2 3 1 4 4 5 5 1 3 6 3 7 3 8 6 1 7 1 8 1
No Yes 3 4 5 6 Yes 3 6 7 8
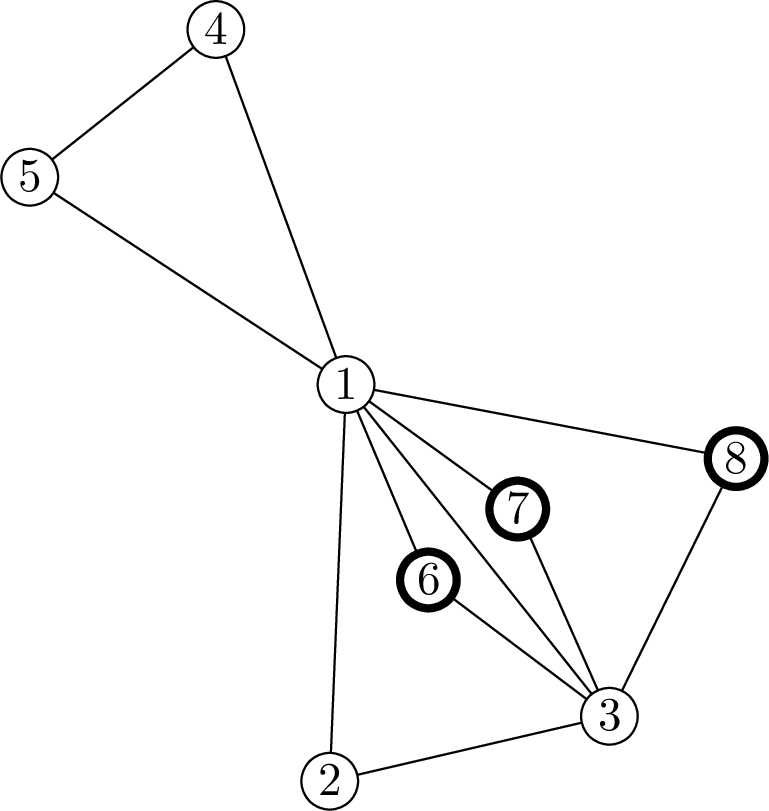
На картинке ниже изображен третий вариант графа из примера. Жирным отмечены вершины, которые может украсть Жулик.
| Название |
|---|




