| Codeforces Round 599 (Div. 1) |
|---|
| Закончено |
Уджан накопил много ненужного хлама в своих ящиках, значительная часть которого является тетрадями с записями по математике: настало время их разобрать. Сейчас он нашёл старую запылившуюся тетрадь по теории графов с описанием одного графа.
Это неориентированный взвешенный граф с $$$n$$$ вершинами. К тому же, это полный граф: каждая пара вершин соединена ребром. Вес каждого ребра равен либо $$$0$$$, либо $$$1$$$; к тому же, ровно $$$m$$$ рёбер имеют вес $$$1$$$, а все остальные рёбра имеют вес $$$0$$$.
Так как Уджан не очень сильно желает разбирать свои записи, он решил найти вес минимального остовного дерева данного графа. (Вес остовного дерева графа равняется сумме весов всех его рёбер.) Можете ли вы найти ответ за Уджана, чтобы он прекратил валять дурака?
Первая строка ввода содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \leq n \leq 10^5$$$, $$$0 \leq m \leq \min(\frac{n(n-1)}{2},10^5)$$$), количество вершин и количество рёбер веса $$$1$$$ в данном графе.
$$$i$$$-тая из следующих $$$m$$$ строк содержит целые числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n$$$, $$$a_i \neq b_i$$$), концы $$$i$$$-го ребра с весом $$$1$$$.
Гарантируется, что ни одно ребро не повторяется во вводе.
Выведите одно целое число, вес минимального остовного дерева в данном графе.
6 11 1 3 1 4 1 5 1 6 2 3 2 4 2 5 2 6 3 4 3 5 3 6
2
3 0
0
Граф из первого примера показан на картинке ниже. Пунктирные рёбра имеют вес $$$0$$$, все остальные рёбра имеют вес $$$1$$$. Одно из возможных остовных деревьев покрашено в оранжевый цвет и имеет общий вес $$$2$$$.
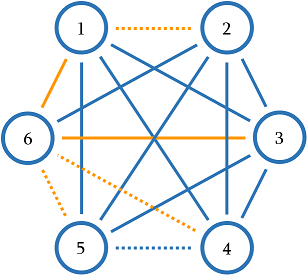
Во втором примере, вес каждого ребра $$$0$$$, поэтому вес любого остовного дерева равен $$$0$$$.
| Название |
|---|




