| Codeforces Round 599 (Div. 1) |
|---|
| Закончено |
Уджан наконец-то убрал свой дом и теперь хочет декорировать интерьер. Он решил приобрести красивый ковёр, который бы по-настоящему украсил гостевую комнату.
Его интересуют ковры, которые состоят из многоугольных частей (граней), где каждая сторона любой части либо является стороной одной другой (отличной) части, либо является внешней стороной. Другими словами, ковёр можно описать как планарный граф, где каждая часть соответствует одной грани, которая является простым многоугольником. Периметр ковра равняется количеству внешних сторон.
Уджан считает ковёр красивым, если он состоит из $$$f$$$ частей, где $$$i$$$-я часть имеет ровно $$$a_i$$$ сторон, и периметр наименьший возможный. Найдите пример такого ковра, чтобы Уджан мог бы его заказать!
Первая строка ввода содержит одно целое число $$$f$$$ ($$$1 \leq f \leq 10^5$$$), количество частей ковра.
Следующая строка содержит $$$f$$$ целых чисел $$$a_1, \ldots, a_f$$$ ($$$3 \leq a_i \leq 3\cdot 10^5$$$), количества сторон каждой части ковра. Общее количество сторон частей $$$a_1 + \ldots + a_f$$$ не превышает $$$3\cdot10^5$$$.
Выведите описание ковра как граф.
Сначала выведите одно целое число $$$n$$$ ($$$3 \leq n \leq 3 \cdot 10^5$$$), общее количество вершин в графе (вершины должны быть пронумерованы числами от $$$1$$$ до $$$n$$$).
Затем выведите $$$f$$$ строк с описанием граней. $$$i$$$-я строка должна содержать описание $$$i$$$-й грани и содержать $$$a_i$$$ различных целых чисел $$$v_{i,1}, \ldots, v_{i,a_i}$$$ ($$$1 \leq v_{i,j} \leq n$$$), что означает, что вершины $$$v_{i,j}$$$ и $$$v_{i,(j \bmod{a_i})+1}$$$ соединены ребром для каждой пары $$$1 \leq j \leq a_i$$$.
Граф должен быть планарным и удовлетворять ограничениям, описанным в условии. Его периметр должен быть наименьшим возможным. Граф не должен содержать кратные рёбра или петли. Граф должен быть связным. Учтите, что решение всегда существует; если существует несколько решений, выведите любое из них.
2 3 3
4 2 1 4 1 2 3
3 5 3 5
6 1 2 3 4 5 4 5 6 1 3 4 6 5
В первом примере, две треугольных грани соединены одним ребром, поэтому периметр получается равным $$$4$$$.
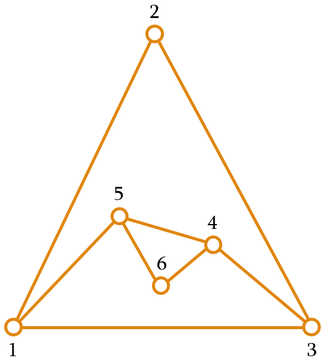
На картинке показана одна возможная конфигурация для второго примера. Наименьший периметр в данном случае равен $$$3$$$.
| Название |
|---|




