| Codeforces Round 592 (Div. 2) |
|---|
| Закончено |
Вам задано дерево, состоящее из $$$n$$$ вершин. Дерево — это связный неориентированный граф, не содержащий циклов.
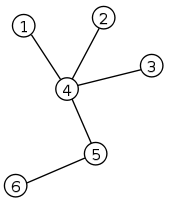Пример дерева. Вы должны покрасить каждую вершину дерева в один из трех цветов. Для каждой вершины известна стоимость ее покраски в каждый из трех цветов.
Вам нужно покрасить все вершины таким образом, чтобы в любом пути, состоящем ровно из трех различных вершин, цвета всех этих трех вершин были различны. Иными словами, рассмотрим все такие тройки вершин $$$(x, y, z)$$$, что $$$x \neq y, y \neq z, x \neq z$$$, вершина $$$x$$$ соединена ребром с вершиной $$$y$$$, а вершина $$$y$$$ соединена ребром с вершиной $$$z$$$. Тогда цвета вершин $$$x$$$, $$$y$$$ и $$$z$$$ должны быть попарно различны. Назовем такую покраску вершин хорошей.
Перед вами стоит задача определить минимальную стоимость хорошей покраски дерева, а также в какой цвет необходимо покрасить каждую из вершин. Если не существует ни одной хорошей покраски дерева, сообщите об этом.
В первой строке следует целое число $$$n$$$ $$$(3 \le n \le 100\,000)$$$ — количество вершин в дереве.
Во второй строке следует последовательность $$$c_{1, 1}, c_{1, 2}, \dots, c_{1, n}$$$ $$$(1 \le c_{1, i} \le 10^{9})$$$, где $$$c_{1, i}$$$ равно стоимости покраски $$$i$$$-й вершины в первый цвет.
В третьей строке следует последовательность $$$c_{2, 1}, c_{2, 2}, \dots, c_{2, n}$$$ $$$(1 \le c_{2, i} \le 10^{9})$$$, где $$$c_{2, i}$$$ равно стоимости покраски $$$i$$$-й вершины во второй цвет.
В четвертой строке следует последовательность $$$c_{3, 1}, c_{3, 2}, \dots, c_{3, n}$$$ $$$(1 \le c_{3, i} \le 10^{9})$$$, где $$$c_{3, i}$$$ равно стоимости покраски $$$i$$$-й вершины в третий цвет.
В каждой из следующих $$$(n - 1)$$$ строк следует по два целых числа $$$u_j$$$ и $$$v_j$$$ $$$(1 \le u_j, v_j \le n, u_j \neq v_j)$$$ — номера вершин, соединенных неориентированным ребром $$$j$$$. Гарантируется, что заданные ребра образуют дерево.
Если не существует хорошей покраски дерева, выведите $$$-1$$$.
В противном случае, в первой строке выведите минимальную стоимость хорошей покраски графа. Во второй строке выведите $$$n$$$ целых чисел $$$b_1, b_2, \dots, b_n$$$ $$$(1 \le b_i \le 3)$$$, где $$$i$$$-е число должно быть равно цвету, в который нужно покрасить вершину $$$i$$$. Если подходящих покрасок минимальной стоимости несколько, разрешается вывести любую из них.
3 3 2 3 4 3 2 3 1 3 1 2 2 3
6 1 3 2
5 3 4 2 1 2 4 2 1 5 4 5 3 2 1 1 1 2 3 2 4 3 5 3
-1
5 3 4 2 1 2 4 2 1 5 4 5 3 2 1 1 1 2 3 2 4 3 5 4
9 1 3 2 1 3
В первом примере три вершины, поэтому все они должны быть покрашены в разные цвета. Первую вершину нужно покрасить в цвет $$$1$$$, вторую вершину — в цвет $$$3$$$, а третью вершину — в цвет $$$2$$$. Стоимость такой покраски равна $$$3 + 2 + 1 = 6$$$.
