| Codeforces Round 595 (Div. 3) |
|---|
| Закончено |
Вам задано дерево, состоящее из $$$n$$$ вершин. Напомним что дерево — это связный неориентированный граф без циклов
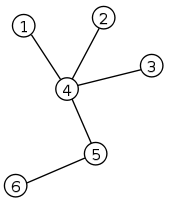Пример дерева. Вершины пронумерованы от $$$1$$$ до $$$n$$$. Все вершины имеют вес, вес вершины $$$v$$$ равен $$$a_v$$$.
Напомним, что дистанция между двумя вершинами в дереве равна количеству ребер на простом пути между ними.
Ваша задача — найти подмножество вершин максимального суммарного веса (вес подмножества равен сумме весов всех вершин в нем) такое, что в этом подмножестве нет пары вершин на расстоянии $$$k$$$ или меньше.
Первая строка входных данных содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n, k \le 200$$$) — количество вершин в дереве и ограничение на расстояние соответственно.
Вторая строка входных данных содержит $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 10^5$$$), где $$$a_i$$$ равно весу вершины $$$i$$$.
Следующие $$$n - 1$$$ строк описывают ребра дерева. Ребро $$$i$$$ описано двумя целыми числами $$$u_i$$$ и $$$v_i$$$ — номерами вершин, которые оно соединяет ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$).
Гарантируется, что заданные ребра образуют дерево.
Выведите одно целое число — максимально возможный суммарный вес подмножества, в котором все пары вершин находятся на расстоянии более $$$k$$$.
5 1 1 2 3 4 5 1 2 2 3 3 4 3 5
11
7 2 2 1 2 1 2 1 1 6 4 1 5 3 1 2 3 7 5 7 4
4
