| Codeforces Round 601 (Div. 1) |
|---|
| Закончено |
Хэнх — известный биолог. Он любит выращивать деревья и проводить эксперименты в своем собственном саду.
Однажды он получил дерево, состоящее из $$$n$$$ вершин. Вершины пронумерованы от $$$1$$$ до $$$n$$$. Дерево с $$$n$$$ вершинами — это неориентированный связный граф с $$$n - 1$$$ ребрами. Первоначально Хэнх устанавливает значение каждой вершины равным $$$0$$$.
Теперь Хэнх выполняет $$$q$$$ запросов, каждых из которых имеет один из следующих типов:
- Тип $$$1$$$: Хэнх выбирает вершину $$$v$$$ и целое число $$$d$$$. Затем он выбирает некоторую вершину $$$r$$$ полностью случайно, и для каждой вершины $$$u$$$ такой, что путь от $$$r$$$ до $$$u$$$ проходит через $$$v$$$, увеличивает значение в вершине $$$u$$$ на $$$d$$$.
- Тип $$$2$$$: Хэнх выбирает вершину $$$v$$$ и считает математическое ожидание значения вершины $$$v$$$.
Поскольку Хэнх биолог, а не математик, ему нужна ваша помощь.
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$1 \leq n, q \leq 150\,000$$$) — количество вершин в дереве Хэнха и количество запросов.
Каждая из следующих $$$n - 1$$$ содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \leq u, v \leq n$$$), которые обозначают, что есть ребро между вершинами $$$u$$$ и $$$v$$$. Гарантируется, что эти $$$n-1$$$ ребра создают дерево.
Каждая из следующих $$$q$$$ строк описывает запросы:
- $$$1$$$ $$$v$$$ $$$d$$$ ($$$1 \leq v \leq n, 0 \leq d \leq 10^7$$$), обозначают первый тип запроса.
- $$$2$$$ $$$v$$$ ($$$1 \leq v \leq n$$$), обозначают второй тип запроса.
Гарантируется, что есть как минимум один запрос второго типа.
Для каждого запроса второго типа выведите математическое ожидание.
Пусть $$$M = 998244353$$$. Можно показать, что ответ может быть представлен в виде несократимой дроби $$$\frac{p}{q}$$$, где $$$p$$$ и $$$q$$$ — целые числа, и $$$q \not \equiv 0 \pmod{M}$$$. Выведите целое число, равное $$$p \cdot q^{-1} \bmod M$$$. Другими словами, выведите такое целое число $$$x$$$, что $$$0 \le x < M$$$ и $$$x \cdot q \equiv p \pmod{M}$$$.
5 12 1 2 1 3 2 4 2 5 1 1 1 2 1 2 2 2 3 2 4 2 5 1 2 2 2 1 2 2 2 3 2 4 2 5
1 199648871 399297742 199648871 199648871 598946614 199648873 2 2 2
Рисунок ниже показывает дерево в примере.
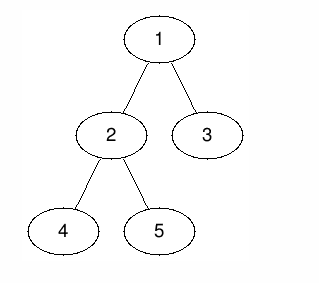
Для первого запроса, где $$$v = 1$$$ и $$$d = 1$$$:
- Если $$$r = 1$$$, значения всех вершин увеличатся.
- Если $$$r = 2$$$, значения вершин $$$1$$$ и $$$3$$$ увеличатся.
- Если $$$r = 3$$$, значения вершин $$$1$$$, $$$2$$$, $$$4$$$ и $$$5$$$ увеличатся.
- Если $$$r = 4$$$, значения вершин $$$1$$$ и $$$3$$$ увеличатся.
- Если $$$r = 5$$$, значения вершин $$$1$$$ и $$$3$$$ увеличатся.
Поэтому математические ожидания вершин после первого запроса такие: ($$$1, 0.4, 0.8, 0.4, 0.4$$$).
Для второго запроса, где $$$v = 2$$$ и $$$d = 2$$$:
- Если $$$r = 1$$$, значения вершин $$$2$$$, $$$4$$$ и $$$5$$$ увеличатся.
- Если $$$r = 2$$$, значения всех вершин увеличатся.
- Если $$$r = 3$$$, значения вершин $$$2$$$, $$$4$$$ и $$$5$$$ увеличатся.
- Если $$$r = 4$$$, значения вершин $$$1$$$, $$$2$$$, $$$3$$$ и $$$5$$$ увеличатся.
- Если $$$r = 5$$$, значения вершин $$$1$$$, $$$2$$$, $$$3$$$ и $$$4$$$ увеличатся.
Поэтому математические ожидания вершин после второго запроса такие: ($$$2.2, 2.4, 2, 2, 2$$$).
| Название |
|---|




