Как видно из названия задачи, вам предстоит решить задачу про отрезки и деревья.
Напомним, что деревом является связный неориентированным граф, такой что между каждой парой его вершин существует ровно один простой путь.
Вам дано $$$n$$$ отрезков $$$[l_1, r_1], [l_2, r_2], \dots, [l_n, r_n]$$$, $$$l_i < r_i$$$ для всех $$$i$$$. Гарантируется, что концы отрезков являются целыми числами, все концы являются уникальными — нет такой пары отрезков, которые начинались бы в одной и той же точке, заканчивались в одной и той же точке, или один бы начинался в такой точке, что другой в ней заканчивается.
Давайте построим граф с $$$n$$$ вершинами. Вершины $$$v$$$ и $$$u$$$ соединены ребром тогда и только тогда, когда отрезки $$$[l_v, r_v]$$$ и $$$[l_u, r_u]$$$ пересекаются и ни один из них не лежит полностью внутри другого.
Например, пары $$$([1, 3], [2, 4])$$$ и $$$([5, 10], [3, 7])$$$ будут образовывать ребра, а пары $$$([1, 2], [3, 4])$$$ и $$$([5, 7], [3, 10])$$$ не будут.
Определите, является ли полученный граф деревом или нет.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 5 \cdot 10^5$$$) — количество отрезков.
$$$i$$$-я из следующих $$$n$$$ строк содержит описание $$$i$$$ отрезка — два целых числа $$$l_i$$$ и $$$r_i$$$ ($$$1 \le l_i < r_i \le 2n$$$).
Гарантируется, что концы всех отрезков попарно различны.
Выведите «YES», если полученный граф является деревом и «NO» в противном случае.
6 9 12 2 11 1 3 6 10 5 7 4 8
YES
5 1 3 2 4 5 9 6 8 7 10
NO
5 5 8 3 6 2 9 7 10 1 4
NO
Граф полученный в первом примере:
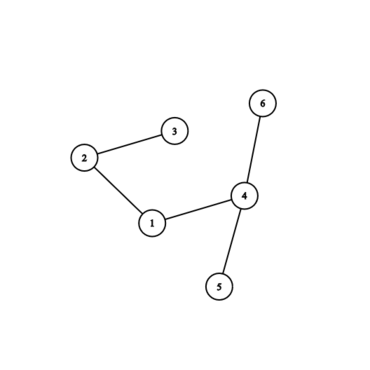
Граф полученный во втором примере:
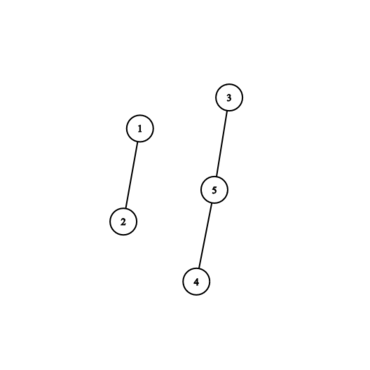
Граф полученный в третьем примере:
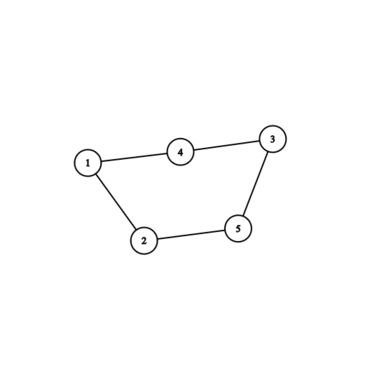
| Название |
|---|




