| Codeforces Round 607 (Div. 1) |
|---|
| Закончено |
Ваш друг Кирхгоф был шокирован текущим состоянием в дизайне электрических схем.
«Боже мой! Что не так с этой областью? Все эти цепи неэффективны! Есть столько возможностей для улучшения. Эти цепи имеют слишком большое полное сопротивление. Почему они сделаны таким образом? Это просто вызывает массовую потерю резисторов! Вся их область могла бы сэкономить так много денег, если бы они просто максимизировали потенциал своих цепей. Почему они не могут просто попробовать альтернативные идеи? Это абсолютно отвратительно» сказал он.
Он очень недоволен ситуацией, но даже после стольких жалоб он все еще не имеет возможности напрямую что-то изменить.
Частота его протестов по поводу электротехники вам надоела, поэтому вы решили взять на себя ответственность и помочь ему самостоятельно. Вы планируете создать программу, которая будет оптимизировать схемы, не меняя при этом схему и сопротивление.
Цепь имеет два конца и соотносится с некоторым параметром $$$R$$$ для этой цепи, который называется сопротивлением.
Цепи, которые мы будем рассматривать будут получены из резисторов. Несколько цепей, среди которых могут быть резисторы, можно соединить вместе последовательно или параллельно, образуя более сложную цепь. Приведенная картинка изображает последовательное и параллельное соединения.
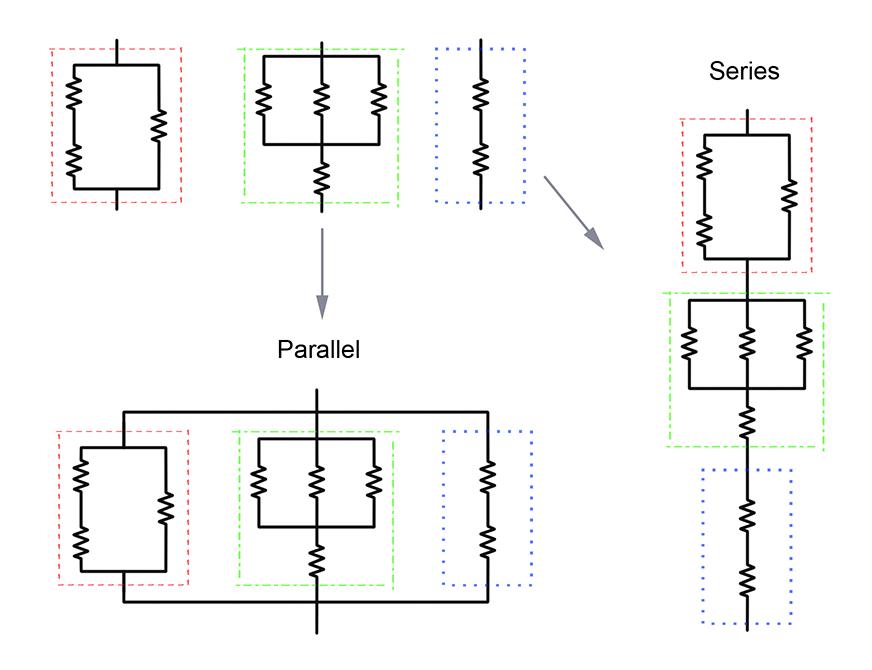
По правилам вашего друга Киргхофа сопротивление может быть легко вычислено при соединении цепей в более сложную цепь следующим способом:
- Когда соединяется $$$k$$$ цепей последовательно с сопротивлениями $$$R_1, R_2, \ldots, R_k$$$, тогда сопротивление $$$R$$$ получившейся цепи будет суммой сопротивлений составляющих ее цепей $$$$$$R = R_1 + R_2 + \ldots + R_k.$$$$$$
- Когда соединяется $$$k$$$ цепей параллельно с сопротивлениями $$$R_1, R_2, \ldots, R_k$$$, тогда сопротивление $$$R$$$ получившейся цепи будет получаться из следующего соотношения на $$$R$$$ $$$$$$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots + \frac{1}{R_k},$$$$$$ если все $$$R_i > 0$$$; если хотя бы одно из $$$R_i = 0$$$, тогда сопротивление получившейся цепи получается равным $$$R = 0$$$.
Цепи будут представлены как строки. Резисторы представляются символом звездочки «*». Для более сложных формул, обозначим строки $$$s_1, s_2, \ldots, s_k$$$, которые представляют $$$k \ge 2$$$ цепей. Тогда
- строка «($$$s_1$$$ S $$$s_2$$$ S $$$\ldots$$$ S $$$s_k$$$)» представляет их последовательное соединение;
- строка «($$$s_1$$$ P $$$s_2$$$ P $$$\ldots$$$ P $$$s_k$$$)» представляет их параллельное соединение.
Например, строка «(* P (* S *) P *)» представляет такую цепь:
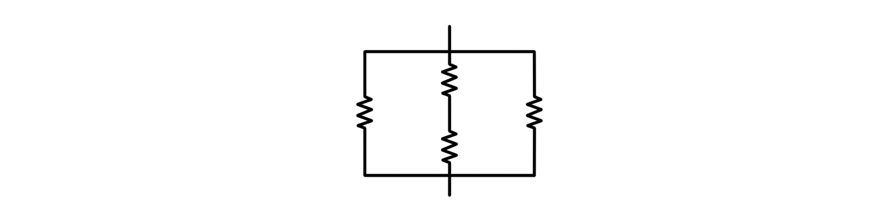
Дана цепь. Ваша задача сопоставить сопротивления всем резисторам, так чтобы были выполнены следующие требования:
- Каждому резистору сопоставлено неотрицательное целое сопротивление;
- Сопротивление всей цепи равно $$$r$$$;
- Сумма сопротивлений всех резисторов минимально возможная.
Если в схеме есть $$$n$$$ резисторов, то вам нужно найти список $$$r_1, r_2, \ldots, r_n$$$ ($$$0 \le r_i$$$, $$$r_i$$$ целое число), где $$$r_i$$$ это сопротивление сопоставленное $$$i$$$-у резистору в строке (слева направо), представляющей данную цепь. Если сделать сопоставление, в котором все условия выполнены невозможно, то сообщите об этом.
Если это сделать возможно, гарантируется, что минимальная сумма сопротивлений всех резисторов не превосходит $$$10^{18}$$$.
В первой строке находится единственное целое число $$$t$$$ ($$$1 \le t \le 32000$$$), количество тестовых случаев. В следующих строках находится описание тестовых случаев.
Для каждого тестового случая в единственной строке находится целое число $$$r$$$ ($$$1 \le r \le 10^6$$$), пробел а затем строка, которая представляет некоторую цепь. Гарантируется, что эта строка корректна по определениям из условия задачи и действительно представляет некоторую цепь. Количество резисторов (символов равных «*») не меньше, чем $$$1$$$ и не больше, чем $$$80000$$$.
Гарантируется что суммарное количество резисторов по всем тестовым случаям не превосходит $$$320000$$$.
Для каждого тестового случая выведите ответ:
- Если возможно получить сопротивление данной цепи, равное $$$r$$$, выведите «REVOLTING» (без кавычек) и затем $$$n$$$ неотрицательных целых чисел $$$r_1, r_2, \ldots, r_n$$$ — сопротивления сопоставленные резисторам. Здесь $$$n$$$ обозначает количество резисторов в цепи.
Если существует несколько возможных сопоставлений с минимальной суммой сопротивлений резисторов, вы можете найти любое из них;
- Если это невозможно выведите единственную строку: «LOSS» (без кавычек).
3 5 * 1 (* S *) 1 (* P (* S *))
REVOLTING 5 REVOLTING 1 0 REVOLTING 2 1 1
Эта картинка иллюстрирует третий тестовый случай:
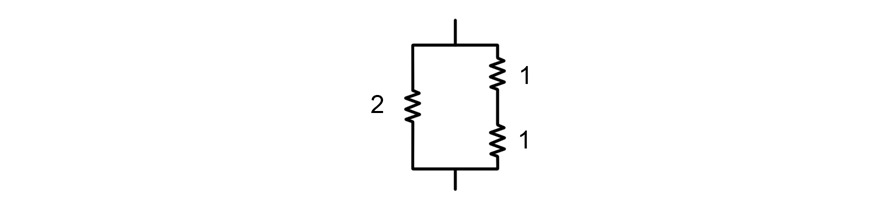
Здесь сумма сопротивлений всех резисторов равна $$$2 + 1 + 1 = 4$$$ и можно показать, что она минимально возможная. Обратите внимание, что существуют другие возможные способы достичь эту минимальную сумму.
| Название |
|---|




