| Codeforces Beta Round 94 (Div. 2 Only) |
|---|
| Закончено |
Аня и Маша ведут математический кружок у шестиклассников. Во время кружка шестиклассники ведут себя плохо. Они принесли на кружок много шнурков, и связались друг с другом. А именно, каждый шнурок связывает вместе двух шестиклассников. При этом, если два шестиклассника связаны шнурком, то шнурок связывает как первого со вторым, так и второго с первым.
Чтобы навести порядок, Аня и Маша делают следующее. Сначала Аня для каждого шестиклассника находит, со сколькими другими шестиклассниками он связан шнурками. Если шестиклассник связан ровно с одним другим, Аня объявляет ему выговор. Потом Маша собирает в группу всех шестиклассников, которым Аня объявила выговор, и выгоняет вон из класса. Выгнанные шестиклассники отвязываются и уходят из класса, забирая с собой шнурки, которыми они были привязаны. Потом снова Аня для каждого шестиклассника находит, со сколькими другими шестиклассниками он связан, и так далее. И так они делают, пока Ане удается объявить хотя бы один выговор.
Определите, сколько групп шестиклассников будут выгнаны из класса.
В первой строке даны два целых числа n и m — исходное число шестиклассников и шнурков (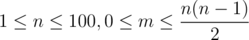
). Шестиклассники пронумерованы числами от 1 до n, а шнурки — числами от 1 до m. В следующих m строках дано по два целых числа a и b — номера шестиклассников, связанных i-ым шнурком (1 ≤ a, b ≤ n, a ≠ b). Гарантируется, что никакие два шестиклассника не связаны более чем одним шнурком. Никакой шнурок не связывает шестиклассника с самим собой.
Выведите единственное число — количество групп шестиклассников, которые будут выгнаны из класса.
3 3
1 2
2 3
3 1
0
6 3
1 2
2 3
3 4
2
6 5
1 4
2 4
3 4
5 4
6 4
1
В первом примере Ане с Машей не выгонят ни одной группы шестиклассников — в изначальной позиции все шестиклассники привязаны к двум другим шестиклассникам, и Ане не удастся сделать ни одного выговора.
Во втором примере четыре шестиклассника связаны в цепочку, а еще два бегают отдельно. Сначала Аня с Машей выгонят двух крайних шестиклассников из цепочки (1 и 4), а затем — двух оставшихся из цепочки (2 и 3). При этом бегающие отдельно от остальных шестиклассники останутся в классе.
В третьем примере Аня с Машей сразу же выгонят всех шестиклассников, кроме четвертого, и на этом процесс закончится. Правильный ответ — один.
