| Codeforces Round 616 (Div. 1) |
|---|
| Закончено |
Вам дано $$$n$$$ попарно неколлинеарных двумерных векторов. Вы можете создавать замкнутые ломаные на двумерной плоскости с помощью этих векторов и следующего процесса:
- Вы встаете в начало координат, точку $$$(0, 0)$$$.
- Выберите один из векторов и отложите отрезок из текущей точки, равный этому вектору. То есть, если ваша текущая точка имеет координаты $$$(x, y)$$$ и вы выбираете вектор $$$(u, v)$$$, нарисуйте отрезок из текущей точки в точку с координатами $$$(x + u, y + v)$$$ и встаньте в точку $$$(x + u, y + v)$$$.
- Повторяйте шаг 2, пока вы не окажетесь в начале координат снова.
Вы можете использовать каждый вектор любое количество раз в ходе процесса.
Посчитайте количество различных, невырожденных (площадь больше $$$0$$$), выпуклых многоугольников, которые могут быть получены этим процессом и такие, что они могут быть помещены в квадрат размером $$$m \times m$$$ и вектора, использованные для построения многоугольника, идут в порядке против часовой стрелки. Поскольку это количество может быть слишком большим вы должны найти его по модулю $$$998244353$$$.
Два многоугольника считаются одинаковыми, если существует параллельный перенос одного из многоугольников, переводящий его в другой.
Многоугольник можно поместить в квадрат размером $$$m \times m$$$, если существует параллельный перенос этого многоугольника, при котором любая точка $$$(u, v)$$$ внутри или на границе получившегося многоугольника удовлетворяет неравенствам $$$0 \leq u, v \leq m$$$.
В первой строке находится два целых числа $$$n$$$ и $$$m$$$ — количество векторов и размер квадрата ($$$1 \leq n \leq 5$$$, $$$1 \leq m \leq 10^9$$$).
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$x_i$$$ и $$$y_i$$$ — $$$x$$$-координата и $$$y$$$-координата $$$i$$$-о вектора ($$$|x_i|, |y_i| \leq 4$$$, $$$(x_i, y_i) \neq (0, 0)$$$).
Гарантируется, что никакие два данных вектора не параллельны, то есть для любых двух индексов $$$i$$$ и $$$j$$$, таких что $$$1 \leq i < j \leq n$$$, не существует вещественного числа $$$k$$$, такого что $$$x_i \cdot k = x_j$$$ и $$$y_i \cdot k = y_j$$$.
Выведите единственное целое число — количество многоугольников, удовлетворяющих всем условиям по модулю $$$998244353$$$.
3 3 -1 0 1 1 0 -1
3
3 3 -1 0 2 2 0 -1
1
3 1776966 -1 0 3 3 0 -2
296161
4 15 -4 -4 -1 1 -1 -4 4 3
1
5 10 3 -4 4 -3 1 -3 2 -3 -3 -4
0
5 1000000000 -2 4 2 -3 0 -4 2 4 -1 -3
9248783
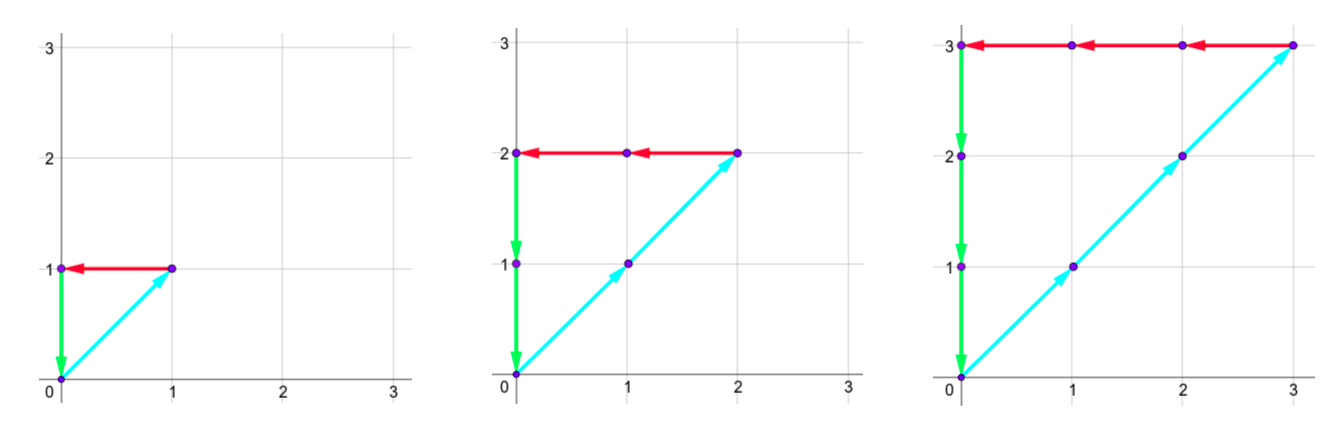
Многоугольники для первого теста:
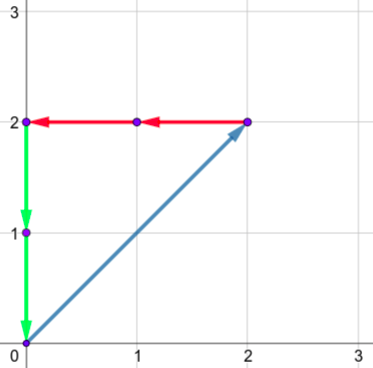
Единственный многоугольник для второго теста:
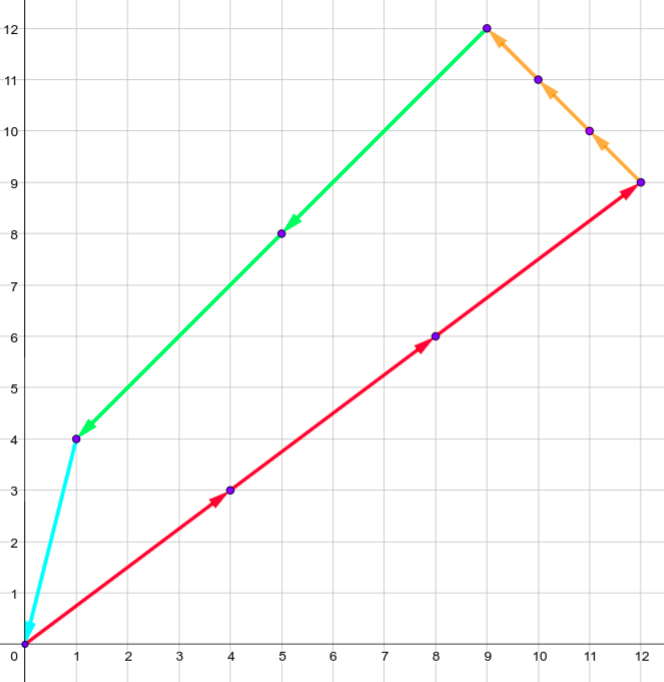
Единственный многоугольник для четвертого теста:
| Название |
|---|




