| Codeforces Round 615 (Div. 3) |
|---|
| Закончено |
Вам задано невзвешенное дерево с $$$n$$$ вершинами. Напомним, что дерево — это связный неориентированный граф без циклов.
Ваша задача — выбрать три различных вершины $$$a, b, c$$$ в этом дереве таких, что количество ребер, принадлежащих как минимум одному из простых путей между $$$a$$$ и $$$b$$$, $$$b$$$ и $$$c$$$, или $$$a$$$ и $$$c$$$, максимально. Обратите внимание на примечания для лучшего понимания.
Простой путь — это путь, который посещает каждую вершину не более одного раза.
Первая строка содержит единственное целое число $$$n$$$ ($$$3 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
Следующая $$$n - 1$$$ строка описывает ребра дерева в виде $$$a_i, b_i$$$ ($$$1 \le a_i$$$, $$$b_i \le n$$$, $$$a_i \ne b_i$$$). Гарантируется, что заданный граф является деревом.
Первой строкой выведите одно целое число $$$res$$$ — максимальное количество ребер, принадлежащих как минимум одному из простых путей между $$$a$$$ и $$$b$$$, $$$b$$$ и $$$c$$$, или $$$a$$$ и $$$c$$$.
Во второй строке выведите три целых числа $$$a, b, c$$$ таких, что $$$1 \le a, b, c \le n$$$ и $$$a \ne, b \ne c, a \ne c$$$.
Если существует несколько подходящих ответов, вы можете вывести любой.
8 1 2 2 3 3 4 4 5 4 6 3 7 3 8
5 1 8 6
Изображение, соответствующее первому примеру (и другой правильный ответ):
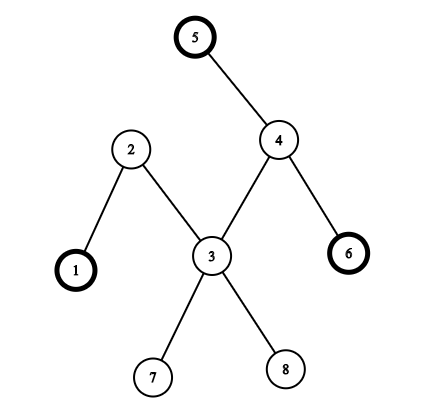
Если выбрать вершины $$$1, 5, 6$$$, то путь между вершинами $$$1$$$ и $$$5$$$ состоит из ребер $$$(1, 2), (2, 3), (3, 4), (4, 5)$$$, путь между $$$1$$$ и $$$6$$$ состоит из ребер $$$(1, 2), (2, 3), (3, 4), (4, 6)$$$ и путь между $$$5$$$ и $$$6$$$ состоит из ребер $$$(4, 5), (4, 6)$$$. Объединение этих путей — $$$(1, 2), (2, 3), (3, 4), (4, 5), (4, 6)$$$, следовательно, ответ — $$$5$$$. Можно показать, что лучшего ответа не существует.
| Название |
|---|




