| Codeforces Round 618 (Div. 1) |
|---|
| Закончено |
Ги-Мануэль и Тома хотят построить космический корабль, являющийся выпуклым многоугольником.
Вам дан строго выпуклый (т. е. никакие три вершины не лежат на одной прямой) многоугольник $$$P$$$, заданный координатами его точек на плоскости. Обозначим как $$$P(x,y)$$$ многоугольник, полученный параллельным переносом $$$P$$$ на вектор $$$\overrightarrow {(x,y)}$$$. Следующий рисунок показывает пример параллельного переноса:
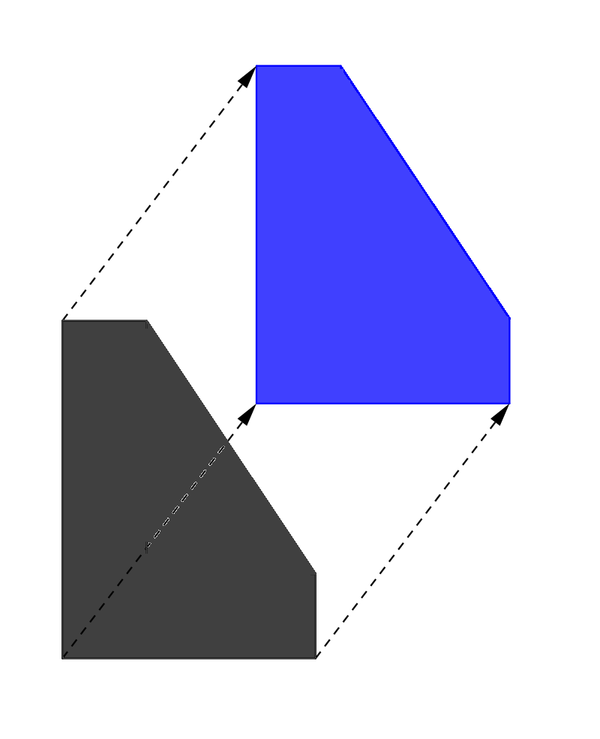
Обозначим как $$$T$$$ множество точек, являющееся объединением всех $$$P(x,y)$$$ таких, что начало координат $$$(0,0)$$$ лежит в $$$P(x,y)$$$ (в том числе и на границе). Также можно дать эквивалентное определение: точка $$$(x,y)$$$ принадлежит $$$T$$$, только если в $$$P$$$ существуют две точки $$$A,B$$$ такие, что $$$\overrightarrow {AB} = \overrightarrow {(x,y)}$$$. Можно показать, что $$$T$$$ тоже является многоугольником. Например, если $$$P$$$ — правильный треугольник, то $$$T$$$ — правильный шестиугольник; на рисунке $$$P$$$ нарисован чёрным цветом, а некоторые $$$P(x,y)$$$, в которых лежит начало координат, нарисованы цветным: 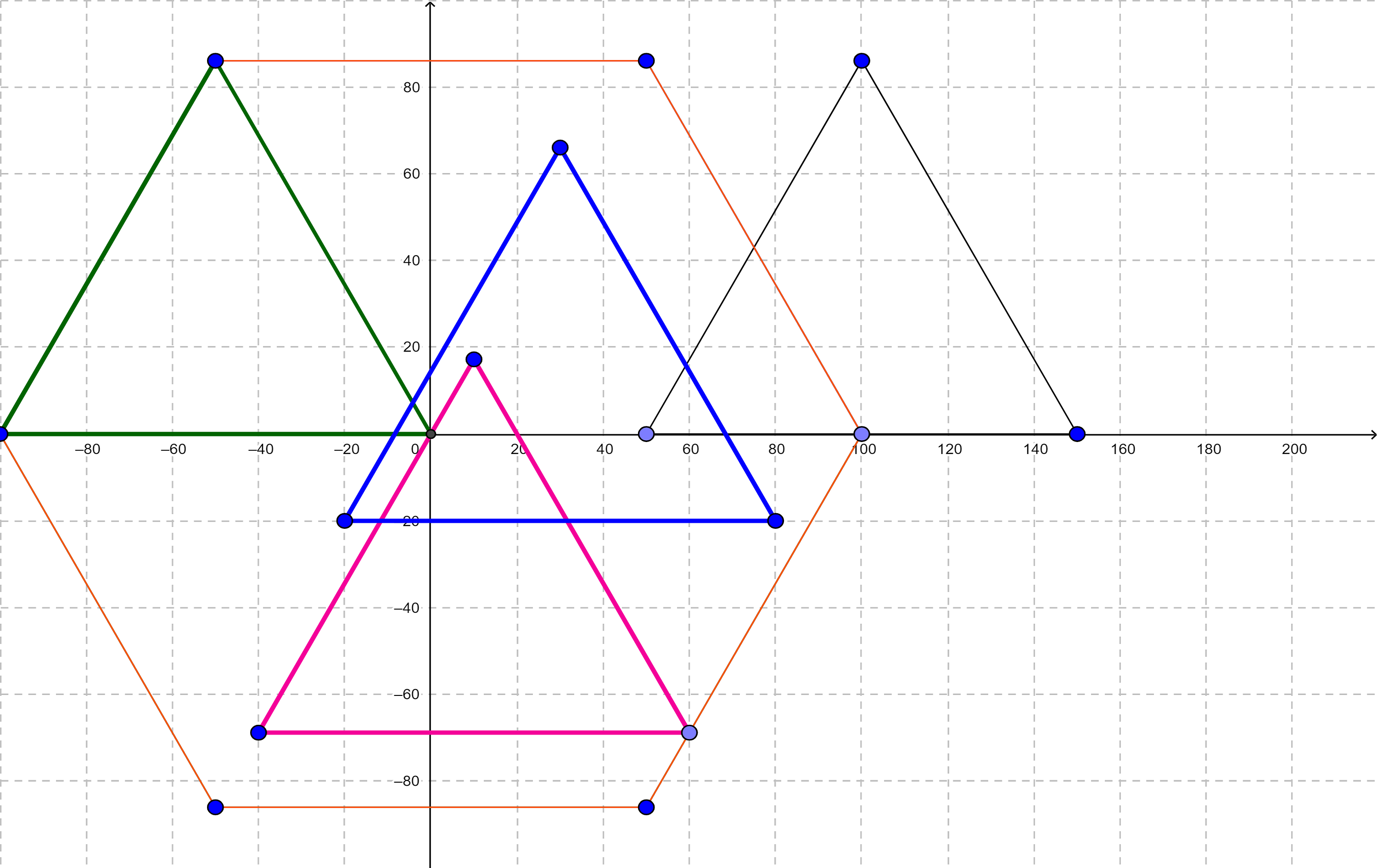 Космический корабль будет иметь наилучшие аэродинамические показатели, если $$$P$$$ и $$$T$$$ подобны. Ваша задача — проверить, что многоугольники $$$P$$$ и $$$T$$$подобны.
Космический корабль будет иметь наилучшие аэродинамические показатели, если $$$P$$$ и $$$T$$$ подобны. Ваша задача — проверить, что многоугольники $$$P$$$ и $$$T$$$подобны.
Первая строка содержит целое число $$$n$$$ ($$$3 \le n \le 10^5$$$) — количество точек.
$$$i$$$-я из следующих $$$n$$$ строк содержит два целых числа $$$x_i, y_i$$$ ($$$|x_i|, |y_i| \le 10^9$$$), обозначающих координаты $$$i$$$-й вершины многоугольника.
Гарантируется, что точки даны в порядке обхода против часовой стрелки, и что они образуют строго выпуклый многоугольник.
Выведите «YES» с новой строки, если $$$P$$$ и $$$T$$$ подобны. Иначе, выведите «NO» с новой строки. Вы можете выводить каждую букву в любом регистре (строчную или заглавную).
4 1 0 4 1 3 4 0 3
YES
3 100 86 50 0 150 0
nO
8 0 0 1 0 2 1 3 3 4 6 3 6 2 5 1 3
YES
На рисунке показан первый тестовый пример: $$$P$$$ и $$$T$$$ — квадраты. Второй пример был разобран в условии. 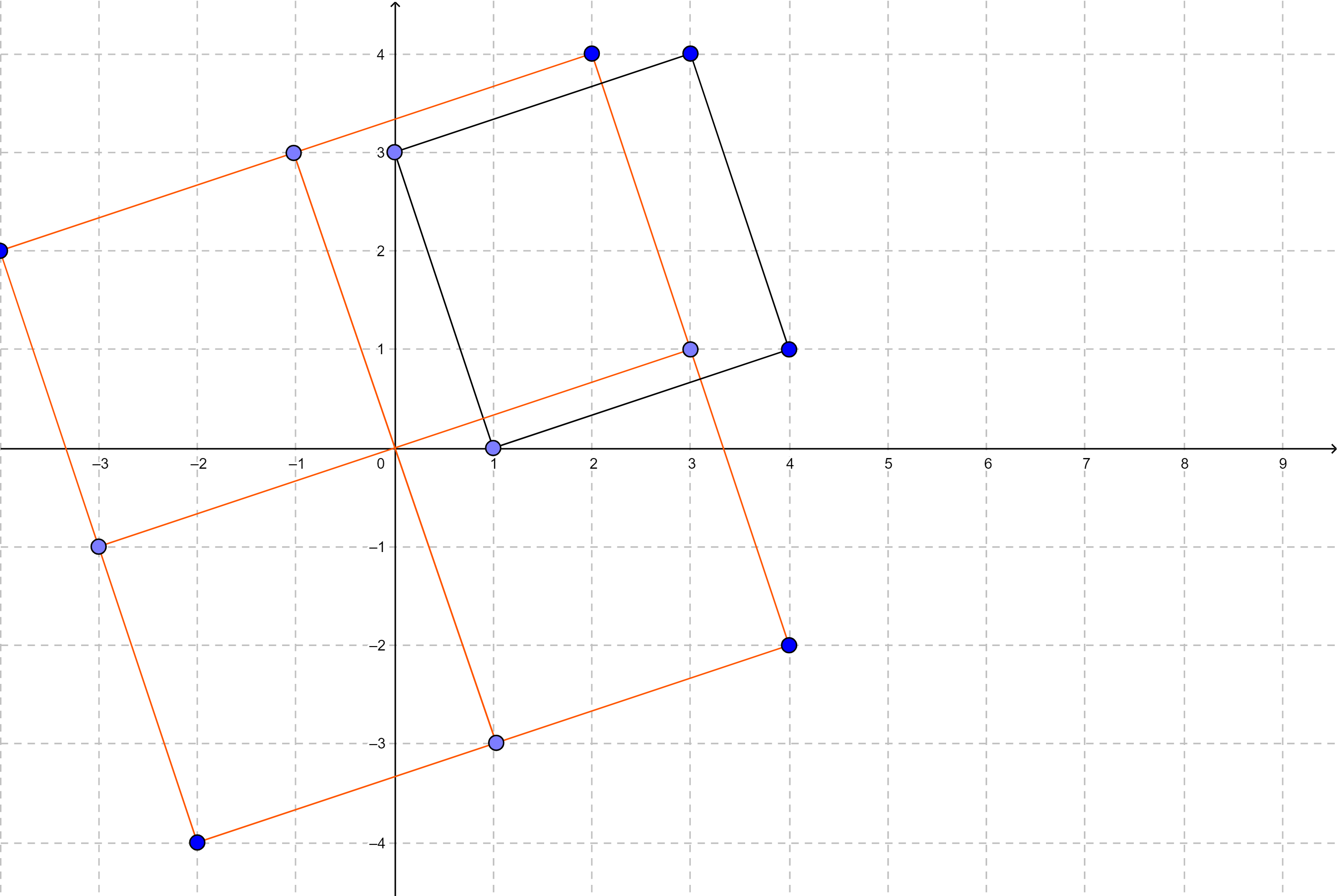
| Название |
|---|




