| Codeforces Round 620 (Div. 2) |
|---|
| Закончено |
Гильдонг забирался на гору, проходя через миллионы деревьев. Вдохновившись ими, он внезапно придумал интересную идею про деревья: А что если мы добавим еще одно ребро в дерево?
Затем, он узнал, что такие древовидные графы называются 1-деревья. Так как Гильдон устал от решения задач на деревья, он решил проверить, могут ли похожие техники для деревьев использованы также для решения задач на 1-деревья. Вместо того, чтобы решать задачти самому, он решил проверить вас, запросами на 1-деревьях.
Сначала, он даст вам дерево (не 1-дерево) на $$$n$$$ вершинах, а затем задаст вам $$$q$$$ запросов. Каждый запрос состоит из $$$5$$$ целых чисел: $$$x$$$, $$$y$$$, $$$a$$$, $$$b$$$, и $$$k$$$. Это означает, что вам надо проверить, есть ли путь из вершины $$$a$$$ в вершину $$$b$$$, которые содержит ровно $$$k$$$ ребер, после добавления двустороннего ребра между вершинами $$$x$$$ и $$$y$$$. Путь может содержать одни и те же вершины и ребра несколько раз. Все запросы независимы друг от друга; т.е. добавленное ребро удаляется для следующего запроса.
Первая строка содержит одно целое число $$$n$$$ ($$$3 \le n \le 10^5$$$), количество вершин в дереве.
Следующие $$$n-1$$$ строки содержат по два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$, $$$u \ne v$$$) каждая, которые означают, что есть ребро между вершинами $$$u$$$ и $$$v$$$. Все ребра неориентированные и различные.
В следующей строке записано одно целое число $$$q$$$ ($$$1 \le q \le 10^5$$$), количество запросов, которое Гильдон хочет вам задать.
Следующие $$$q$$$ строк содержат по пять целых чисел $$$x$$$, $$$y$$$, $$$a$$$, $$$b$$$, и $$$k$$$ каждая ($$$1 \le x,y,a,b \le n$$$, $$$x \ne y$$$, $$$1 \le k \le 10^9$$$) — целые числа, описанные в условии. Гарантируется, что ребра между вершинами $$$x$$$ и $$$y$$$ не было в исходном дереве.
Для каждого запроса, выведите «YES» если есть путь, который содержит ровно $$$k$$$ ребер, от $$$a$$$ до $$$b$$$, после добавления неориентированного ребра между вершинами $$$x$$$ и $$$y$$$. Иначе, выведите «NO».
Вы можете выводить все буквы в любом регистре (верхнем или нижнем).
5 1 2 2 3 3 4 4 5 5 1 3 1 2 2 1 4 1 3 2 1 4 1 3 3 4 2 3 3 9 5 2 3 3 9
YES YES NO YES NO
Следующая картинка описывает дерево (кружочки и отрезки) и добавленные ребра для каждого запроса (пунктирные линии).
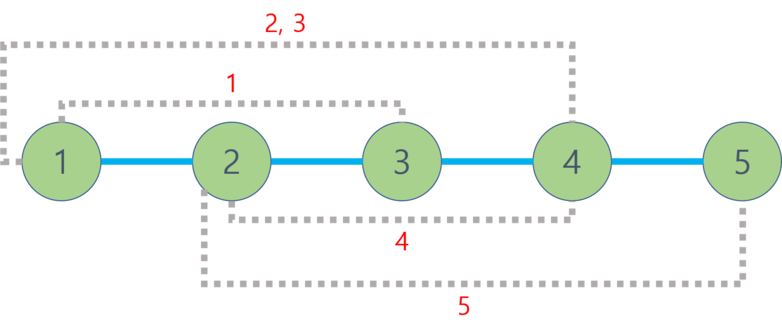
Возможные пути для ответов «YES»:
- $$$1$$$-й запрос: $$$1$$$ – $$$3$$$ – $$$2$$$
- $$$2$$$-й запрос: $$$1$$$ – $$$2$$$ – $$$3$$$
- $$$4$$$-й запрос: $$$3$$$ – $$$4$$$ – $$$2$$$ – $$$3$$$ – $$$4$$$ – $$$2$$$ – $$$3$$$ – $$$4$$$ – $$$2$$$ – $$$3$$$
| Название |
|---|




