| Codeforces Round 621 (Div. 1 + Div. 2) |
|---|
| Закончено |
У Бесси действительно много друзей, потому что она — всеми любимая корова! Ее новый друг Кролик пытается допрыгать до Бесси, чтобы поиграть вместе!
Точнее, он хочет попасть из $$$(0,0)$$$ в $$$(x,0)$$$, сделав несколько прыжков. Он готов прыгнуть из одной точки в другую на плоскости только если евклидово расстояние между этими точками равно одному из $$$n$$$ его любимых чисел: $$$a_1, a_2, \ldots, a_n$$$. За какое минимальное количество прыжков Кролик сможет добраться из $$$(0,0)$$$ в $$$(x,0)$$$? Кролик может приземляться, в том числе, и в точки с нецелочисленными координатами. Можно доказать, что Кролик всегда может достигнуть точки назначения.
Напомним, что евклидово расстояние между точками $$$(x_i, y_i)$$$ и $$$(x_j, y_j)$$$ равно $$$\sqrt{(x_i-x_j)^2+(y_i-y_j)^2}$$$.
Например, если любимые числа Кролика — это $$$1$$$ и $$$3$$$, то он может добраться из $$$(0,0)$$$ в $$$(4,0)$$$ за два прыжка (как показано ниже). Заметим, что существуют и другие способы добраться до $$$(4,0)$$$ за $$$2$$$ прыжка (например, $$$(0,0)$$$ $$$\rightarrow$$$ $$$(2,-\sqrt{5})$$$ $$$\rightarrow$$$ $$$(4,0)$$$).
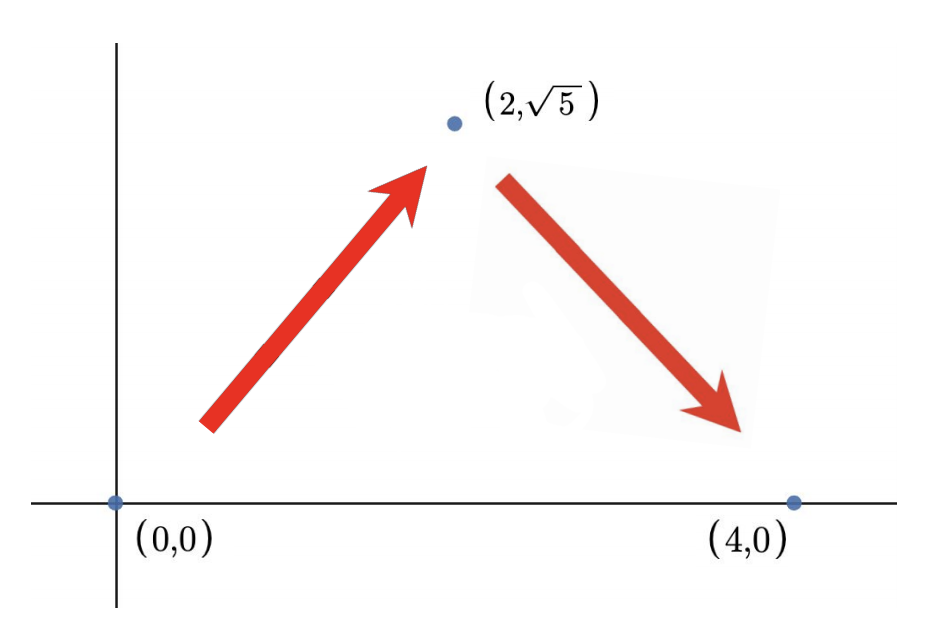Изображение соответствует первому набору входных данных из примера. Длина обоих прыжков равна $$$3$$$, одному из любимых чисел Кролика. Таким образом, перед каждым прыжком Кролик выбирает одно из чисел $$$a_i$$$ и прыгает из текущей точки на расстояние ровно $$$a_i$$$ в произвольном направлении. Одно и то же число он может выбирать любое количество раз.
Входные данные состоят из нескольких наборов входных данных. В первой строке задано единственное число $$$t$$$ ($$$1 \le t \le 1000$$$) — количество наборов входных данных. В следующих $$$2t$$$ строках заданы сами наборы — по две строки на набор.
В первой строке каждого набора задано два целых числа $$$n$$$ и $$$x$$$ ($$$1 \le n \le 10^5$$$, $$$1 \le x \le 10^9$$$) — количество любимых чисел и расстояние, которое необходимо преодолеть Кролику соответственно.
Во второй строке каждого набора задано $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le 10^9$$$) — любимые числа Кролика. Гарантируется, что все любимые числа различны.
Гарантируется, что сумма $$$n$$$ по всем наборам не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите единственное число — минимальное необходимое количество прыжков.
42 41 33 123 4 51 552 1015 4
2 3 1 2
Первый набор изображен на рисунке выше. Кролик может прыгнуть сначала в $$$(2,\sqrt{5})$$$, а потом в $$$(4,0)$$$ — суммарно два прыжка. Каждый прыжок имеет длину $$$3$$$ — одно из его любимых чисел.
Во втором наборе, одним из способов добраться за $$$3$$$ прыжка является: $$$(0,0)$$$ $$$\rightarrow$$$ $$$(4,0)$$$ $$$\rightarrow$$$ $$$(8,0)$$$ $$$\rightarrow$$$ $$$(12,0)$$$.
В третьем наборе, Кролик может прыгнуть из $$$(0,0)$$$ в $$$(5,0)$$$.
В четвертом наборе, Кролик может прыгать так: $$$(0,0)$$$ $$$\rightarrow$$$ $$$(5,10\sqrt{2})$$$ $$$\rightarrow$$$ $$$(10,0)$$$.
