| Codeforces Round 624 (Div. 3) |
|---|
| Закончено |
Вам даны два целых числа $$$n$$$ и $$$d$$$. Нужно построить корневое бинарное дерево из $$$n$$$ вершин с корнем в вершине $$$1$$$ с суммой глубин всех вершин равной $$$d$$$.
Дерево — это связный граф без циклов. Корневое дерево имеет специальную вершину — корень. Родитель вершины $$$v$$$ — это последняя отличная от $$$v$$$ вершина на пути от корня к вершине $$$v$$$. Глубина вершины $$$v$$$ — это длина пути от корня к вершине $$$v$$$. Дети вершины $$$v$$$ — все вершины, для которых $$$v$$$ является родителем. Бинарное дерево — это такое дерево, в котором ни одна вершина не имеет более $$$2$$$ детей.
Вам нужно ответить на $$$t$$$ независимых наборов входных данных.
Первая строка теста содержит одно целое число $$$t$$$ ($$$1 \le t \le 1000$$$) — количество наборов входных данных.
Единственная строка каждого набора содержит два целых числа $$$n$$$ и $$$d$$$ ($$$2 \le n, d \le 5000$$$) — количество вершин в дереве и требуемую сумму глубин всех вершин.
Гарантируется, что сумма всех $$$n$$$ и сумма всех $$$d$$$ не превышают $$$5000$$$ ($$$\sum n \le 5000, \sum d \le 5000$$$).
Для каждого набора входных данных выведите ответ на него.
Если невозможно построить такое дерево, выведите «NO» (без кавычек) первой строкой. Иначе выведите «{YES}» первой строкой. Затем выведите $$$n-1$$$ целое число $$$p_2, p_3, \dots, p_n$$$ второй строкой, где $$$p_i$$$ — родитель вершины $$$i$$$. Обратите внимание: последовательность родителей, которую вы выведете, должна описывать некоторое бинарной дерево.
3 5 7 10 19 10 18
YES 1 2 1 3 YES 1 2 3 3 9 9 2 1 6 NO
Изображения, соответствующие первому и второму наборам входных данных из примера:
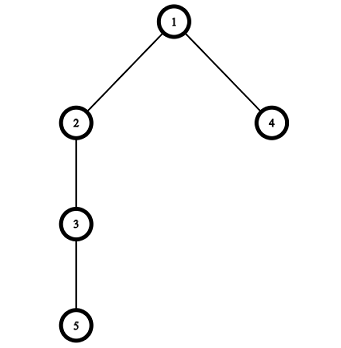
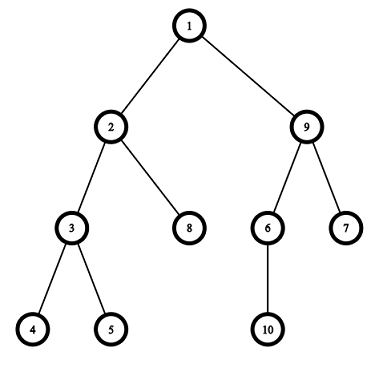
| Название |
|---|




