Вам задано два целых числа $$$n$$$ и $$$m$$$ ($$$m < n$$$). Рассмотрим выпуклый правильный многоугольник на $$$n$$$ вершинах. Напомним, что правильный многоугольник — это многоугольник, у которого все углы равны между собой и все стороны равны между собой.
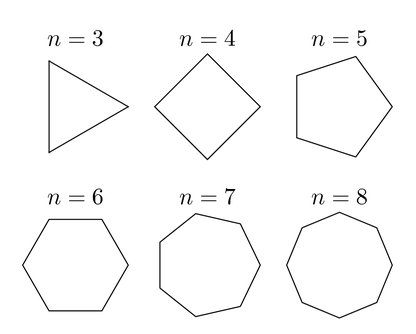 Примеры выпуклых правильных многоугольников
Примеры выпуклых правильных многоугольников Ваша задача — узнать, возможно ли построить другой выпуклый правильный многоугольник на $$$m$$$ вершинах такой, что его центр совпадает с центром изначального многоугольника, а каждая его вершина является какой-то вершиной изначального многоугольника.
Вам необходимо ответить на $$$t$$$ независимых наборов тестовых данных.
Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов тестовых данных.
Следующие $$$t$$$ строк описывают наборы тестовых данных. Каждый набор тестовых данных задан двумя целыми числами $$$n$$$ и $$$m$$$, разделенных пробелом ($$$3 \le m < n \le 100$$$) — количеством вершин в изначальном многоугольнике и количеством вершин в многоугольнике, который вы хотите построить.
Выведите ответ на каждый набор тестовых данных — «YES» (без кавычек), если возможно построить другой выпуклый правильный многоугольник на $$$m$$$ вершинах такой, что его центр совпадает с центром изначального многоугольника, а каждая его вершина является какой-то вершиной изначального многоугольника, и «NO» в противном случае.
2 6 3 7 3
YES NO
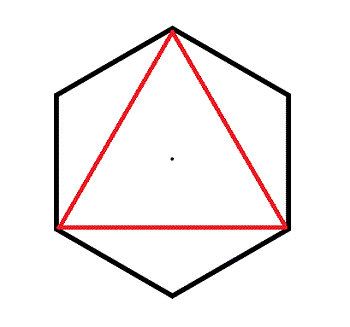 Первый набор тестовых данных из примера
Первый набор тестовых данных из примера Можно показать, что ответ на второй набор тестовых данных из примера равен «NO».
| Название |
|---|




