| CodeCraft-20 (Div. 2) |
|---|
| Закончено |
Нэш придумал интересную, но простую игру, где игрок просто должен выполнять инструкции, написанные на клетке, где игрок сейчас стоит.
В эту игру играют на доске $$$n\times n$$$. Строки и столбцы этой доски пронумерованны от $$$1$$$ до $$$n$$$. Клетку на пересечении $$$r$$$-й строки и $$$c$$$-го столбца будем обозначать, как $$$(r, c)$$$.
Некоторые клетки этой доски называются заблокированными зонами. На каждой клетке доски написан один из следующих $$$5$$$ символов — $$$U$$$, $$$D$$$, $$$L$$$, $$$R$$$ или $$$X$$$ — инструкции для игрока. Пусть текущая клетка — $$$(r, c)$$$. Если символ в клетке $$$R$$$, игрок должен переместиться в клетку справа, $$$(r, c+1)$$$, для $$$L$$$ игрок должен переместиться в клетку слева, $$$(r, c-1)$$$, для $$$U$$$ игрок должен переместиться в клетку выше, $$$(r-1, c)$$$, для $$$D$$$ игрок должен переместиться в клетку ниже, $$$(r+1, c)$$$. Если же символ в клетке равен $$$X$$$, то эта клетка является заблокированной зоной. Игрок должен оставаться в этой клетке (и с этого момента игра для него не слишком интересна).
Гарантируется, что символы записаны таким образом, что игрок никогда не будет вынужден сойти с доски, в какой бы клетке он не начал.
Когда игрок начинает в какой-то клетке, он должен двигаться в соответствии с символом в текущей клетке. Игрок двигается до тех пор, пока он не попадет в заблокированную зону. Может оказаться так, что игрок будет двигаться бесконечно долго.
Для каждой из $$$n^2$$$ клеток таблицы Алиса, ваш друг, хотела бы узнать, как пройдет игра, если игрок начнет в этой клетке. Для каждой стартовой клетки доски, она запишет клетку, в которой игрок остановится, или то, что игрок никогда не остановится. Она предоставила вам эту информацию: для каждой клетки $$$(r, c)$$$ она написала:
- пару ($$$x$$$,$$$y$$$), значащую, что если игрок начинает в клетке $$$(r, c)$$$, то он остановится в клетке ($$$x$$$,$$$y$$$).
- или пару ($$$-1$$$,$$$-1$$$), значащую, что если игрок начинает в клетке $$$(r, c)$$$, он будет двигаться бесконечно долго, и никогда не попадет в заблокированную зону.
Возможно, Алиса хочет вас обмануть, и не существует доски, которая удовлетворяет всей информации, которую она вам предоставила. Для данной информации, восстановите подходящую доску, или определите, что ее не существует. Если существует несколько подходящих досок, вы можете найти любую из них.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \leq n \leq 10^{3}$$$) — сторону доски.
$$$i$$$-я из последующих $$$n$$$ строк содержит $$$2n$$$ чисел $$$x_1, y_1, x_2, y_2, \dots, x_n, y_n$$$, где $$$(x_j, y_j)$$$ ($$$1 \leq x_j \leq n, 1 \leq y_j \leq n$$$, или $$$(x_j,y_j)=(-1,-1)$$$) — пара, записанная Алисой для клетки $$$(i, j)$$$.
Если не существует доски, удовлетворяющей информации, которую вам дала Алиса, выведите INVALID.
Иначе, выведите VALID. В $$$i$$$-й из следующих $$$n$$$ строк, выведите строку из $$$n$$$ символов, соответствующих $$$i$$$-й строке найденной вами подходящей доски. Каждый символ должен быть равен $$$U$$$, $$$D$$$, $$$L$$$, $$$R$$$ или $$$X$$$. Если существует несколько подходящих досок, вы можете найти любую из них.
2 1 1 1 1 2 2 2 2
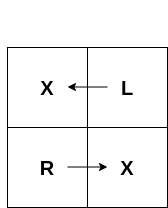
VALID XL RX
3 -1 -1 -1 -1 -1 -1 -1 -1 2 2 -1 -1 -1 -1 -1 -1 -1 -1
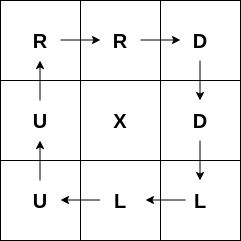
VALID RRD UXD ULL
В первом примере:
Доска с вывода подходит.
- Если игрок начинает в $$$(1,1)$$$, он не будет двигаться, следуя $$$X$$$, и останется там.
- Если игрок начинает в $$$(1,2)$$$, он пойдет влево, следуя $$$L$$$, и остановится в $$$(1,1)$$$.
- Если игрок начинает в $$$(2,1)$$$, он пойдет вправо, следуя $$$R$$$, и остановится в $$$(2,2)$$$.
- Если игрок начинает в $$$(2,2)$$$, он не будет двигаться, следуя $$$X$$$, и останется там.
Ходы игрока для разных клеток изображены на картинке ниже:
Во втором примере:
Доска с вывода подходит, так как игрок, начавший с клетки, отличной от центральной клетки $$$(2,2)$$$, будет двигаться по циклу и никогда не остановится. Если бы он начал в $$$(2,2)$$$, он бы там и остался, следуя инструкции $$$X$$$ .
Ходы игрока для разных клеток изображены на картинке ниже:
| Название |
|---|




