Задано целое положительное число $$$D$$$. Построим из него следующий граф:
- каждая вершина является делителем $$$D$$$ (не обязательно простым, $$$1$$$ и $$$D$$$ тоже включаются);
- между двумя вершинами $$$x$$$ и $$$y$$$ ($$$x > y$$$) есть неориентированное ребро, если $$$x$$$ делится на $$$y$$$ и $$$\frac x y$$$ — простое число;
- вес ребра — это количество делителей $$$x$$$, которые не являются делителями $$$y$$$.
Например, граф для $$$D=12$$$:
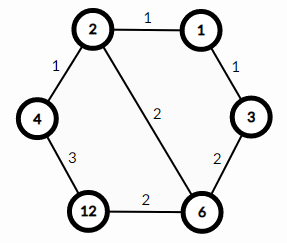
У ребра $$$(4,12)$$$ вес $$$3$$$, потому что у $$$12$$$ делители $$$[1,2,3,4,6,12]$$$, а у $$$4$$$ делители $$$[1,2,4]$$$. Поэтому существует $$$3$$$ делителя $$$12$$$, которые не являются делителями $$$4$$$ — $$$[3,6,12]$$$.
Между $$$3$$$ и $$$2$$$ нет ребра, потому что $$$3$$$ не делится на $$$2$$$. Между $$$12$$$ и $$$3$$$ нет ребра, потому что $$$\frac{12}{3}=4$$$ не простое число.
Длина пути между некоторыми вершинами $$$v$$$ и $$$u$$$ в графе равна сумме весов ребер в нем. Например, длина пути $$$[(1, 2), (2, 6), (6, 12), (12, 4), (4, 2), (2, 6)]$$$ равен $$$1+2+2+3+1+2=11$$$. Длина пустого пути равна $$$0$$$.
Тогда кратчайший путь между двумя вершинами $$$v$$$ и $$$u$$$ — это путь, длина которого минимальна.
Два пути $$$a$$$ и $$$b$$$ различны, если либо содержат различное количество ребер, либо существует такая позиция $$$i$$$, что ребра $$$a_i$$$ и $$$b_i$$$ различны.
Даны $$$q$$$ запросов вида:
- $$$v$$$ $$$u$$$ — посчитайте количество кратчайших путей между вершинами $$$v$$$ и $$$u$$$.
Ответ может быть довольно большим, поэтому выведите его по модулю $$$998244353$$$.
В первой строке записано одно целое число $$$D$$$ ($$$1 \le D \le 10^{15}$$$) — число, из которого строится граф.
Во второй строке записано одно целое число $$$q$$$ ($$$1 \le q \le 3 \cdot 10^5$$$) — количество запросов.
В каждой из следующих $$$q$$$ строк записаны два целых числа $$$v$$$ и $$$u$$$ ($$$1 \le v, u \le D$$$). Гарантируется, что $$$D$$$ делится и на $$$v$$$, и на $$$u$$$ (и $$$v$$$, и $$$u$$$, являются делителями $$$D$$$).
Выведите $$$q$$$ целых чисел — для каждого запроса выведите количество кратчайших путей между двумя данными вершинами по модулю $$$998244353$$$.
12 3 4 4 12 1 3 4
1 3 1
1 1 1 1
1
288807105787200 4 46 482955026400 12556830686400 897 414 12556830686400 4443186242880 325
547558588 277147129 457421435 702277623
В первом примере:
- на первый запрос только пустой путь — длина $$$0$$$;
- на второй запрос пути $$$[(12, 4), (4, 2), (2, 1)]$$$ (длина $$$3+1+1=5$$$), $$$[(12, 6), (6, 2), (2, 1)]$$$ (длина $$$2+2+1=5$$$) и $$$[(12, 6), (6, 3), (3, 1)]$$$ (длина $$$2+2+1=5$$$).
- на третий запрос только путь $$$[(3, 1), (1, 2), (2, 4)]$$$ (длина $$$1+1+1=3$$$).
| Название |
|---|




