| Codeforces Round 633 (Div. 1) |
|---|
| Закончено |
Благодаря успеху TWICE, JYP Entertainment заработала бесчисленные деньги и стала крупнейшей развлекательной компанией по рыночной капитализации. Поэтому начальник JYP решил создать новую нацию и назначил вас предоставить схему проектирования.
Новая нация состоит из $$$n$$$ городов и нескольких дорог между ними. JYP дал некоторые ограничения:
- Чтобы гарантировать эффективность, избегая хаоса, для любых $$$2$$$ разных городов $$$A$$$ и $$$B$$$, между ними существует ровно одна дорога, и она является однонаправленной. Нет дорог, соединяющих город с самим собой.
- Логотип конкурирующих компаний не должен появляться в плане, а именно: там не существует $$$4$$$ различных городов $$$A$$$, $$$B$$$, $$$C$$$, $$$D$$$ таких, что выполняется следующая конфигурация.
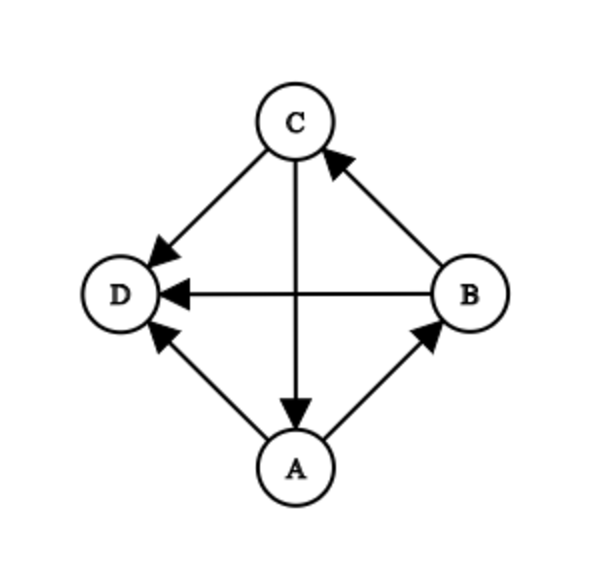
JYP дал критерии для вашей диаграммы. Для двух городов $$$A$$$, $$$B$$$, через $$$dis(A,B)$$$ обозначим наименьшее число дорог, которое вам нужно пройти, чтобы пройти от $$$A$$$ до $$$B$$$. Если невозможно пройти от $$$A$$$ к $$$B$$$, $$$dis(A,B) = 614n$$$. Затем значение эффективности определяется как сумма $$$dis(A,B)$$$ по всем упорядоченным парам различных городов $$$(A,B)$$$.
Обратите внимание, что $$$dis(A,B)$$$ не обязательно должно быть равно $$$dis(B,A)$$$.
Вы нарисовали схему проекта, которая удовлетворяет ограничениям JYP. Найдите сумму $$$dis(A,B)$$$ по всем упорядоченным парам городов $$$(A,B)$$$ с $$$A\neq B$$$.
Обратите внимание, что ввод дается в сжатом виде. Но даже хотя он сжат, лучше используйте быстрое считывание.
Первая строка содержит одно целое число $$$n$$$ ($$$4 \le n \le 8000$$$, $$$n \equiv 0 \pmod{4}$$$) — количество городов.
Далее следует описание матрицы. В каждой из $$$n$$$ следующих строк следуют по $$$\frac{n}{4}$$$ однозначных чисел шестнадцатеричной системы счисления (то есть, эти числа могут задаваться либо как цифры от $$$0$$$ до $$$9$$$, либо как прописные латинские буквы от $$$A$$$ до $$$F$$$). Двоичная запись каждого из этих чисел задаёт очередные $$$4$$$ элемента матрицы в текущей строке. Например, если число равно $$$B$$$, то очередные четыре элемента матрицы равны $$$1011$$$, а если число равно $$$5$$$, то очередные четыре элемента матрицы равны $$$0101$$$.
После того, как вы получите расшифрованную двоичную матрицу, $$$j$$$-й символ $$$i$$$-й строки будет равен $$$1$$$, если односторонняя дорога между городами $$$i$$$ и $$$j$$$ направлена от $$$i$$$ к $$$j$$$, и $$$0$$$ в противном случае. Гарантируется, что граф удовлетворяет ограничениям, указанным выше.
Выведите одно целое число, равное сумме $$$dis(A,B)$$$ по всем упорядоченным парам городов $$$(A,B)$$$ с $$$A\neq B$$$.
4 7 2 1 4
7380
8 7F 3F 1F 0C 06 03 11 18
88464
Первый пример соответствует матрице:
$$$\begin{matrix} 0111 \\ 0010 \\ 0001 \\ 0100 \\ \end{matrix}$$$
Которая соответствует следующему графу:
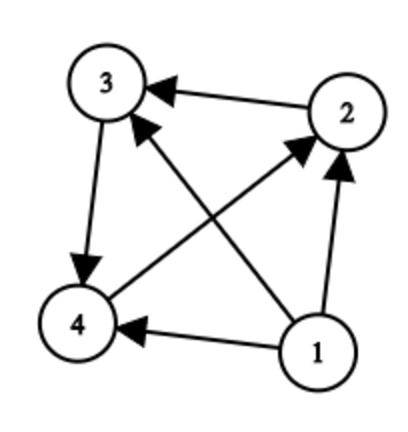
$$$dis(1,2)=dis(1,3)=dis(1,4)=dis(2,3)=dis(3,4)=dis(4,2)=1$$$
$$$dis(2,4)=dis(4,3)=dis(3,2)=2$$$
$$$dis(2,1)=dis(3,1)=dis(4,1)=2456$$$
Поэтому ответ на диаграмму составляет $$$7380$$$.
| Название |
|---|




