| Codeforces Round 633 (Div. 2) |
|---|
| Закончено |
У вас есть целое число $$$n$$$. Сколькими способами можно полностью покрыть поясоподобную область, состоящую из $$$4n-2$$$ треугольников, ромбами?
Ромб состоит из двух треугольников. Вы можете перемещать, вращать или переворачивать ромб, но вы не можете масштабировать его.
$$$2$$$ покрытия называются различными, если некоторые $$$2$$$ треугольника покрыты одним и тем же ромбом в одном из них, и различными в другом.
Пожалуйста, посмотрите на иллюстрации ниже для лучшего понимания.
 Слева изображен ромб, которым вы будете заполнять область, а справа — область, которую вы хотите заполнить.
Слева изображен ромб, которым вы будете заполнять область, а справа — область, которую вы хотите заполнить.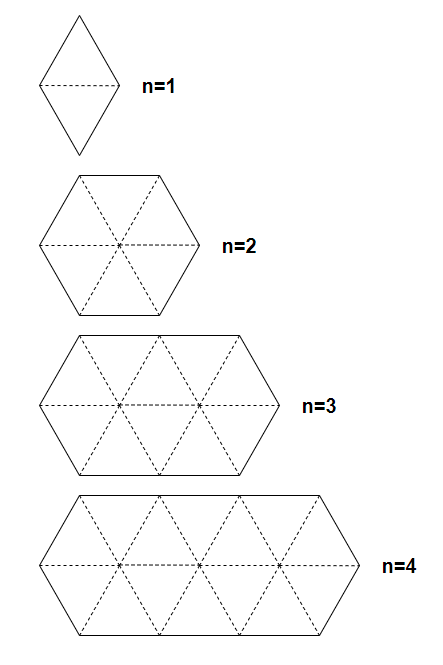 Выше приведены области, для $$$n = 1, 2, 3, 4$$$.
Выше приведены области, для $$$n = 1, 2, 3, 4$$$.
Вы должны ответить на $$$t$$$ независимых тестовых случаев.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^{4}$$$) — количество тестовых случаев.
Каждая из следующих $$$t$$$ строк содержит одно целое число $$$n$$$ ($$$1 \le n \le 10^{9}$$$).
Для каждого теста выведите количество способов полностью покрыть поясоподобную область, состоящую из $$$4n-2$$$ треугольников, ромбами. Можно показать, что при данных ограничениях это количество не превышает $$$10^{18}$$$.
2 2 1
2 1
В первом тестовом примере, есть следующие $$$2$$$ способа заполнить область:
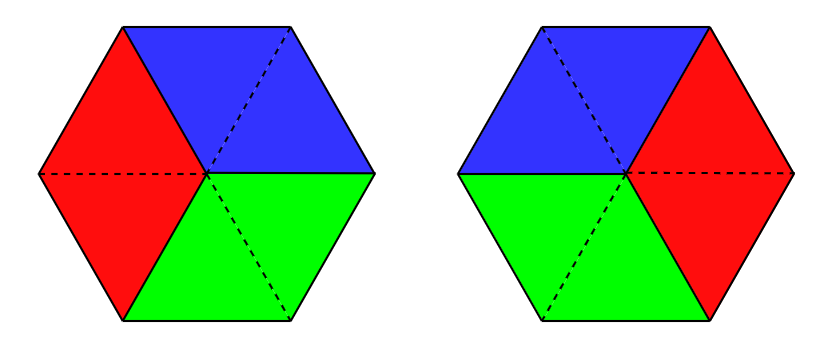
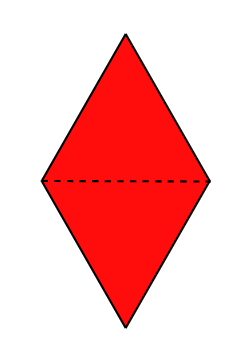
Во втором тестовом примере, существует единственный способ заполнить область:
| Название |
|---|




