| Codeforces Round 639 (Div. 1) |
|---|
| Закончено |
Однополюсный магнит — это магнит, у которого ровно один полюс: либо северный, либо южный. Они не существуют в природе, потому что настоящие магниты имеют два полюса, но это задача по программированию, поэтому будем считать, что такие магниты существуют.
У вас есть таблица размером $$$n\times m$$$. Изначально вы можете поставить несколько магнитов с северным полюсом и несколько магнитов с южным полюсом в некоторые клетки этой таблицы. Вам разрешено расставлять сколько угодно магнитов, в том числе несколько в одну клетку.
Можно выполнять следующую операцию: выбрать один магнит с северным полюсом и один магнит с южным полюсом для активации. Если они находятся в одной строке или в одном столбце, но занимают разные клетки, то магнит с северным полюсом переместится на одну клетку ближе к магниту с южным полюсом. Иначе, если они занимают одинаковые клетки или не находятся в одной строке или в одном столбце, то ничего не произойдет. Обратите внимание, что магниты с южным полюсом неподвижны.
Каждая клетка таблицы покрашена в черный или белый цвет. Будем рассматривать расстановки магнитов в таблице, для которых следующие условия будут выполнены.
- В каждой строке и каждом столбце таблицы находится хотя бы один магнит с южным полюсом.
- Если клетка таблицы черная, тогда можно переместить какой-нибудь магнит с северным полюсом в эту клетку с помощью некоторой последовательности операций из начального расположения магнитов.
- Если клетка таблицы белая, тогда никакой магнит с северным полюсом невозможно переместить в эту клетку с помощью некоторой последовательности операций из начального расположения магнитов.
Определите, можно ли расположить магниты в таблице так, что все условия будут выполнены. Если это возможно, найдите минимальное количество магнитов с северным полюсом, которое для этого требуется (минимизировать количество магнитов с южным полюсом не нужно).
В первой строке находятся два целых числа $$$n$$$ и $$$m$$$ ($$$1\le n,m\le 1000$$$) — количество строк и столбцов в таблице, соответственно.
Следующие $$$n$$$ строк описывают раскраску таблицы: $$$i$$$-я из этих строк содержит строку длины $$$m$$$, в которой $$$j$$$-й символ обозначает цвет клетки таблицы, находящейся в строке $$$i$$$ и столбце $$$j$$$. Символы «#» и «.» обозначают черный и белый цвета соответственно. Гарантируется, что строка не содержит других символов.
Выведите единственное целое число, которое равно минимальному количеству магнитов с северным полюсом, которое требуется.
Если не существует способа расставить магниты, который будет удовлетворять всем условиям, выведите единственное целое число $$$-1$$$.
3 3 .#. ### ##.
1
4 2 ## .# .# ##
-1
4 5 ....# ####. .###. .#...
2
2 1 . #
-1
3 5 ..... ..... .....
0
В первом тесте возможно расположить магниты следующим образом:
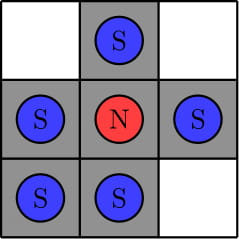
Во втором тесте можно показать, что не существует необходимых расположений магнитов. На следующей картинке показаны три примера расположений, которые удовлетворяют не всем условиям. Первый пример нарушает правило $$$3$$$, потому что мы можем переместить магнит с северным полюсом вниз на белую клетку. Второй пример нарушает правило $$$2$$$, потому что мы не можем переместить магнит с северным полюсом в левую нижнюю черную клетку никакой последовательностью операций. Третий пример нарушает правило $$$1$$$, потому что нет ни одного магнита с южным полюсом в первом столбце.
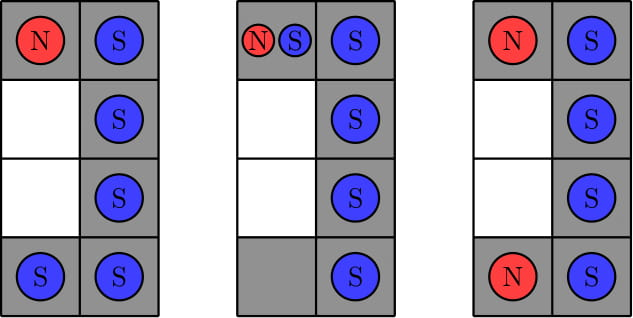
Следующая картинка показывает пример возможного расположения магнитов в третьем тесте. Можно показать, что не существует необходимых расположений магнитов с меньшим количеством магнитов с северным полюсом.
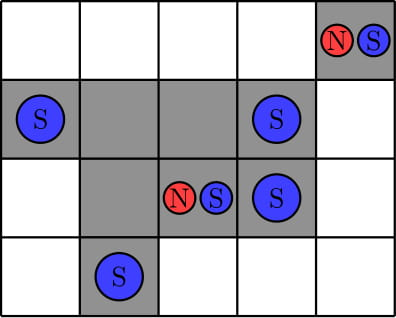
Во четвертом тесте можно показать, что не существует необходимых расположений магнитов. На следующей картинке два примера расположений, которые удовлетворяют не всем условиям. Первый пример нарушает правило $$$1$$$, потому что нет ни одного магнита с южным полюсом в первой строке. Второй пример нарушает правила $$$1$$$ и $$$3$$$, потому что нет ни одного магнита с южным полюсом во второй строке, а кроме того, мы можем переместить магнит с северным полюсом на одну клетку вверх, и он попадет на белую клетку.
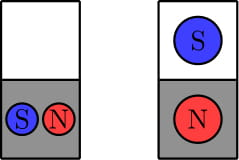
В пятом тесте мы можем поставить магниты с южным полюсом во все клетки и не использовать ни одного магнита с северным полюсом. Поскольку нет ни одной черной клетки, это будет корректной расстановкой магнитов.
| Название |
|---|




