| Codeforces Round 649 (Div. 2) |
|---|
| Закончено |
Для связного неориентированного графа с $$$n$$$ вершинами и целого числа $$$k$$$, вы должны, на ваш выбор:
- или найти независимое множество с ровно $$$\lceil\frac{k}{2}\rceil$$$ вершинами.
- или найти простой цикл длины не более $$$k$$$.
Независимое множество — это набор вершин такой, что никакие две из них не связаны ребром. Простой цикл — это цикл, который не содержит ни одной вершины дважды.
У меня есть доказательство, что для любых входных данных вы всегда можете решить по крайней мере одну из этих задач, но оно слишком тривиально, чтобы поместиться здесь.
Первая строка содержит три целых числа $$$n$$$, $$$m$$$, and $$$k$$$ ($$$3 \le k \le n \le 10^5$$$, $$$n-1 \le m \le 2 \cdot 10^5$$$) — количество вершин и ребер в графе и параметр $$$k$$$ из условия.
Каждая из следующих $$$m$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), которые обозначают, что между вершинами $$$u$$$ и $$$v$$$ есть ребро. Гарантируется, что граф связен и не содержит петель или кратных ребер.
Если вы решили решить первую задачу, то в первой строке выведите $$$1$$$, а затем строку, содержащую $$$\lceil\frac{k}{2}\rceil$$$ различных целых чисел, не превышающих $$$n$$$ — вершины в желаемом независимом наборе.
Если же вы решили решить вторую задачу, то в первой строке выведите $$$2$$$, затем строку, содержащую одно целое число, $$$c$$$, представляющее длину найденного цикла, а затем строку, содержащую $$$c$$$ различных целых чисел, не превышающих $$$n$$$ — вершины в нужном цикле, в порядке их появления в цикле.
4 4 3 1 2 2 3 3 4 4 1
1 1 3
4 5 3 1 2 2 3 3 4 4 1 2 4
2 3 2 3 4
4 6 3 1 2 2 3 3 4 4 1 1 3 2 4
2 3 1 2 3
5 4 5 1 2 1 3 2 4 2 5
1 1 4 5
В первом примере:
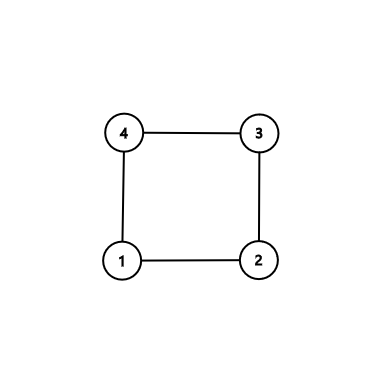
Обратите внимание, что вывод независимого множества $$$\{2,4\}$$$ тоже зачтется, но вывод цикла $$$1-2-3-4$$$ — нет, потому что его длина должна быть не более $$$3$$$.
Во втором примере:
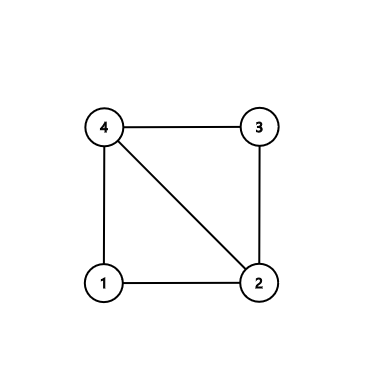
Обратите внимание, что вывод независимого множества $$$\{1,3\}$$$ или цикла $$$2-1-4$$$ также зачтутся.
В третьем примере:
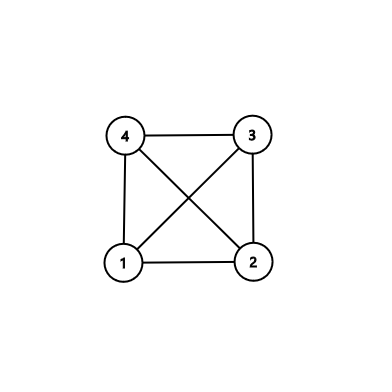
В четвертом примере:
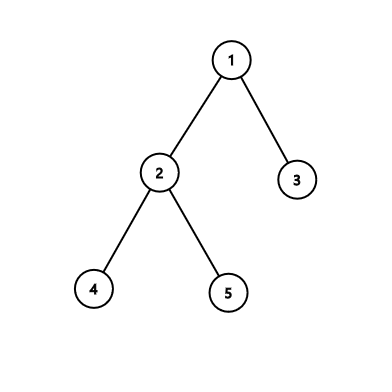
| Название |
|---|




