Задан простой взвешенный связный неориентированный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер.
Путем длины $$$k$$$ в графе назовем последовательность из $$$k+1$$$ вершины $$$v_1, v_2, \dots, v_{k+1}$$$ такую, что для каждого $$$i$$$ $$$(1 \le i \le k)$$$ ребро $$$(v_i, v_{i+1})$$$ присутствует в графе. У пути из вершины $$$v$$$ вершина $$$v_1=v$$$. Обратите внимание, что вершины и ребра могут входить в путь по несколько раз.
Вес пути — это сумма весов ребер в нем.
Для каждого $$$i$$$ от $$$1$$$ до $$$q$$$ рассмотрим путь из вершины $$$1$$$ длины $$$i$$$ максимального веса. Чему равна сумма весов этих $$$q$$$ путей?
Ответ может быть довольно большим, поэтому выведите его по модулю $$$10^9+7$$$.
В первой строке записаны три целых числа $$$n$$$, $$$m$$$, $$$q$$$ ($$$2 \le n \le 2000$$$; $$$n - 1 \le m \le 2000$$$; $$$m \le q \le 10^9$$$) — количество вершин в графе, количество ребер в графе и количество длин, которые надо учесть в ответе.
В каждой из следующих $$$m$$$ строк задано описание ребра: три целых числа $$$v$$$, $$$u$$$, $$$w$$$ ($$$1 \le v, u \le n$$$; $$$1 \le w \le 10^6$$$) — две вершины $$$v$$$ и $$$u$$$ соединены неориентированным ребром веса $$$w$$$. Граф не содержит петель и кратных ребер. Гарантируется, что данные ребра задают связный граф.
Выведите одно целое число — сумма весов путей максимального веса из вершины $$$1$$$ длин $$$1, 2, \dots, q$$$ по модулю $$$10^9+7$$$.
7 8 25 1 2 1 2 3 10 3 4 2 1 5 2 5 6 7 6 4 15 5 3 1 1 7 3
4361
2 1 5 1 2 4
60
15 15 23 13 10 12 11 14 12 2 15 5 4 10 8 10 2 4 10 7 5 3 10 1 5 6 11 1 13 8 9 15 4 4 2 9 11 15 1 11 12 14 10 8 12 3 6 11
3250
5 10 10000000 2 4 798 1 5 824 5 2 558 4 1 288 3 4 1890 3 1 134 2 3 1485 4 5 284 3 5 1025 1 2 649
768500592
Граф из первого примера:
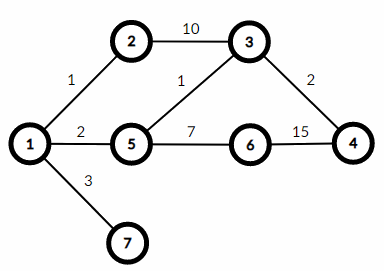
Некоторые максимальные пути:
- длина $$$1$$$: ребра $$$(1, 7)$$$ — вес $$$3$$$;
- длина $$$2$$$: ребра $$$(1, 2), (2, 3)$$$ — вес $$$1+10=11$$$;
- длина $$$3$$$: ребра $$$(1, 5), (5, 6), (6, 4)$$$ — вес $$$2+7+15=24$$$;
- длина $$$4$$$: ребра $$$(1, 5), (5, 6), (6, 4), (6, 4)$$$ — вес $$$2+7+15+15=39$$$;
- $$$\dots$$$
Поэтому ответ — это сумма $$$25$$$ слагаемых: $$$3+11+24+39+\dots$$$
Во втором примере веса у путей максимального веса равны $$$4$$$, $$$8$$$, $$$12$$$, $$$16$$$ and $$$20$$$.
| Название |
|---|




