| Codeforces Global Round 8 |
|---|
| Закончено |
Это более сложная версия задачи H с запросами на изменение.
Лестер и Делберт работают в компании-производителе электроники. Сейчас они трудятся над микроплатой, которая должен соединять две независимые части большого суперкомпьютера.
Плата строится на основе макета в виде сетки. В макете $$$n$$$ рядов и $$$m$$$ столбцов, и на каждом пересечении ряда и столбца находится контакт. Также, на каждой из сторон макета расположены порты, которые можно подсоединять к ближайшему контакту. На левой и правой стороне находится по $$$n$$$ портов, а на верхней и нижней — по $$$m$$$ портов. Каждый из портов снаружи соединён с одной из частей суперкомпьютера, и раскрашен в красный либо синий цвет.
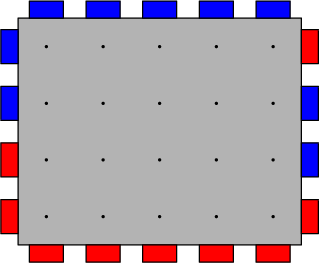
Порты можно соединять проводами внутри платы. Однако, есть несколько требований:
- Каждый провод должен соединять красный и синий порт, и каждый порт может быть соединён не более чем одним проводом.
- Каждый участок провода должен быть горизонтальным либо вертикальным, и повороты возможно только в одном из контактов.
- Чтобы избежать интерференции, провода не должны иметь общих частей ненулевой длины (однако, они могут проходить через общие контакты). Кроме того, провод не может покрывать один участок ненулевой длины дважды.
Пропускной способностью платы называется наибольшее количество соединений между красными и синими портами, которого можно достичь, соблюдая условия выше. Например, плата, изображенная выше, имеет пропускную способность $$$7$$$, и один из способов построить семь соединений изображён ниже.
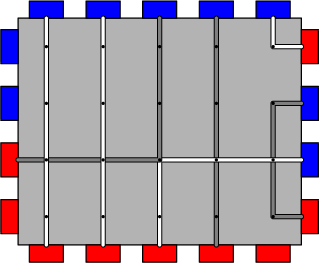
До этого места условия обеих версий задачи совпадают. Различия начинаются ниже.
Как это часто бывает, спецификации проекта в ходе разработки часто меняются, поэтому цвета всех портов ещё не установлены окончательно. Приходит $$$q$$$ модификаций, каждая из которых выглядит так: «цвета всех портов на непрерывном отрезке вдоль одной из сторон меняются на противоположные (красные на синий, синие на красный)». Предыдущие модификации не отменяются перед тем, как происходит следующая.
Чтобы оценить критичность изменений, Лестер и Делберт должны узнать пропускную способность платы после каждой модификации. Помогите им сделать это эффективно.
В первой строке записано три целых числа $$$n, m, q$$$ ($$$1 \leq n, m \leq 10^5$$$, $$$0 \leq q \leq 10^5$$$) — количество рядов и столбцов в макете, и количество изменений соответственно.
Следующие четыре строки описывают исходные цвета портов. Каждый символ в этих строках равен R или B в зависимости от цвета соответствующего порта. Первые две из этих строк содержат по $$$n$$$ символов и описывают сверху вниз порты на левой и правой стороне соответственно. Следующие две строки содержат по $$$m$$$ символов и описывают слева направо порты на верхней и нижней стороне соответственно.
Следующие $$$q$$$ строк описывают модификации. Каждая из этих строк содержит символ $$$s$$$, а затем два целых числа $$$l$$$ и $$$r$$$. Если $$$s$$$ равен L или R, то модификация затрагивает левую/правую сторону соответственно, тогда $$$l$$$ и $$$r$$$ удовлетворяют $$$1 \leq l \leq r \leq n$$$, и порты в рядах с $$$l$$$ по $$$r$$$ (включительно) на соответствующей стороне меняют цвет. Аналогично, если $$$s$$$ равен U или D, то $$$1 \leq l \leq r \leq m$$$, и порты в столбцах с $$$l$$$ по $$$r$$$ (включительно) на верхней/нижней стороне соответственно меняют цвет.
Выведите $$$q + 1$$$ число по одному на строке — пропускную споособность платы после применения $$$0, \ldots, q$$$ модификаций к исходной раскраске портов.
4 5 4 BBRR RBBR BBBBB RRRRR L 2 3 R 3 4 U 1 5 D 1 5
7 7 9 4 9
| Название |
|---|




