| Codeforces Round 651 (Div. 2) |
|---|
| Закончено |
Обратите внимание, что единственное различие между простой и сложной версиями задачи заключается в количестве разрешенных запросов. Вы можете делать взломы, только если все версии задачи решены.
Это интерактивная задача.
Вам дано дерево, состоящее из $$$n$$$ вершин, пронумерованных целыми числами от $$$1$$$ до $$$n$$$. Ayush и Ashish выбрали две секретные различные вершины дерева. Вам нужно отгадать обе вершины. Вы можете делать следующий запрос:
- Вы даете список вершин дерева и в результате получаете вершину из списка, сумма растояний от которой до двух загаданных вершин минимально (если таких вершин в списке несколько, вы получите одну из них). Вы также получите сумму расстояний от этой вершины до двух загаданных вершин.
Напомним, что деревом называется связный граф без циклов. Расстоянием между двумя вершинами называется количество ребер, лежащих на простом пути между ними.
Более формально, пусть две загаданные вершины это $$$s$$$ и $$$f$$$. За один запрос, вы можете дать множество вершин $$$\{a_1, a_2, \ldots, a_c\}$$$ дерева. В результате вы получите два числа $$$a_i$$$ и $$$dist(a_i, s) + dist(a_i, f)$$$. Вершина $$$a_i$$$ является любой вершиной из данного вами множества, для которой число $$$dist(a_i, s) + dist(a_i, f)$$$ минимально.
Вы можете сделать не более $$$14$$$ запросов.
В первой строке находится единственное целое число $$$t$$$ $$$(1 \leq t \leq 10)$$$ — количество наборов входных данных. Обратите внимание на то, как организован процесс взаимодействия.
В первой строке каждого набора входных данных находится единственное целое число $$$n$$$ $$$(2 \le n \le 1000)$$$ — количество вершин дерева.
В следующих $$$n - 1$$$ строках находится по два целых числа $$$u$$$, $$$v$$$ $$$(1 \le u, v \le n, u \ne v)$$$ — ребра дерева.
Для того, чтобы сделать запрос, выведите единственную строку в следующем формате:
- В начале строки выведите «? c » (без кавычек), где $$$c$$$ $$$(1 \leq c \leq n)$$$ равно количеству вершин в списке, про который вы хотите сделать запрос. После этого должны следовать $$$c$$$ различных целых чисел из отрезка $$$[1, n]$$$ — номера вершин из списка.
В ответ на запрос, вы получите два целых числа $$$x$$$, $$$d$$$ — вершина (из вершин из списка из запроса) с минимальной суммой расстояний до двух загаданных вершин и сумма расстояний от этой вершины до двух загаданных вершин. Если список вершин в запросе некорректный или вы превысили лимит на количество запросов, вы получите $$$x = d = -1$$$. В этом случае, вы должны завершить вашу программу немедленно.
После того, как вы угадаете загаданные вершины, выведите единственную строку «! » (без кавычек). После этого выведите два целых числа из отрезка $$$[1, n]$$$ — загаданные вершины. Вы можете выводить их в любом порядке.
После этого, вы должны считать строку. Если вы угадали вершины правильно, вы получите строку «Correct». В этом случае вы должны продолжить решать оставшиеся наборы входных данных или завершить программу, если все наборы входных данных были решены. Иначе, вы получите строку «Incorrect». В этом случае, вы должны завершить программу немедленно.
Запрос угадывания загаданных вершин не считается в количестве сделанных запросов.
Интерактор не адаптивный. Загаданные вершины не меняются во время запросов.
Не забывайте считать строку «Correct» / «Incorrect» после запроса угадывания вершин.
Вы должны решить набор входных данных перед получением входных данных следующего набора входных данных.
Ограничение на $$$14$$$ запросов существует для каждого набора входных данных по отдельности, а не для всех входных данных вместе.
После вывода запроса, не забывайте выводить символ переноса строки и сбрасывать буфер выходного потока. Иначе, вы получите вердикт Idleness limit exceeded. Чтобы это сделать, используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- обратитесь к документации для других языков.
Взломы
Чтобы сделать взлом, используйте следующий формат теста:
В первой строке должно находиться единственное целое число $$$t$$$ $$$(1 \leq t \leq 10)$$$ — количество наборов входных данных. Затем должно следовать описание наборов входных данных.
Первая строка каждого набора входных данных должна содержать единственное целое число $$$n$$$ $$$(2 \le n \le 1000)$$$ — количество вершин в дереве. Во второй строке должно находиться два различных целых числа из отрезка $$$[1, n]$$$ — загаданные вершины. Следующая $$$n - 1$$$ строка должна содержать по два целых числа $$$u$$$, $$$v$$$ $$$(1 \le u, v \le n, u \ne v)$$$ — ребра дерева.
1 3 1 2 1 3 1 1 2 3 3 1 3 1 Correct
? 1 1 ? 1 2 ? 1 3 ? 2 2 3 ! 1 3
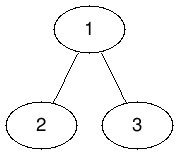
Дерево из первого теста изображено на картинке, загаданные вершины $$$1$$$ и $$$3$$$.
| Название |
|---|




