| Codeforces Round 658 (Div. 1) |
|---|
| Закончено |
В игре «Гениальный шифр» есть два игрока — Алиса и Боб. У Алисы есть секретный код, который Боб хочет отгадать. Код определяется последовательностью из $$$n$$$ цветов. Всего существует $$$n+1$$$ цвет, они пронумерованы целыми числами от $$$1$$$ до $$$n+1$$$.
После того как Боб сделал свою догадку, Алиса говорит ему некоторую информацию о том, насколько его код правильный, в виде двух целых чисел $$$x$$$ и $$$y$$$.
Первое число $$$x$$$ равно количеству индексов, в которых цвет кода Боба совпал с правильным цветом в коде Алисы. Второе число $$$y$$$ равно размеру пересечения двух кодов, как мультимножеств. Другими словами, если Боб может поменять порядок цветов в его догадке, $$$y$$$ равно максимальному количеству правильных индексов, которое он сможет получить.
Например, допустим $$$n=5$$$, код Алисы будет $$$[3,1,6,1,2]$$$ и догадка Боба будет $$$[3,1,1,2,5]$$$. В позициях $$$1$$$ и $$$2$$$ цвета совпали, тогда как в других позициях нет. Поэтому $$$x=2$$$. И два кода имеют четыре общих цвета $$$1,1,2,3$$$, поэтому $$$y=4$$$.
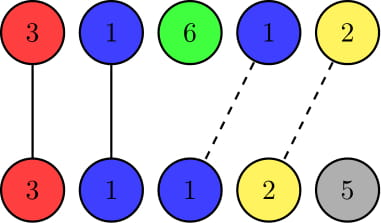 Обычные линии обозначают совпадающие цвета на одинаковых позициях. Пунктирные линии обозначают одинаковые цвета на разных позициях. Тогда $$$x$$$ равно количеству обычных линий и $$$y$$$ равно количеству всех линий.
Обычные линии обозначают совпадающие цвета на одинаковых позициях. Пунктирные линии обозначают одинаковые цвета на разных позициях. Тогда $$$x$$$ равно количеству обычных линий и $$$y$$$ равно количеству всех линий. Вам дан код-догадка Боба и два значения $$$x$$$ и $$$y$$$. Можете ли вы найти какой-то возможный загаданный код Алисы, такой что числа $$$x$$$ и $$$y$$$ будут правильными?
В первой строке находится единственное целое число $$$t$$$ ($$$1\le t\le 1000$$$) — количество наборов входных данных. Следующие $$$2t$$$ строк содержат описания наборов входных данных.
В первой строке каждого набора входных данных находится три целых числа $$$n,x,y$$$ ($$$1\le n\le 10^5, 0\le x\le y\le n$$$) — длины кодов и два числа, которые сказала Алиса.
Во второй строке каждого набора входных данных находится $$$n$$$ целых чисел $$$b_1,\ldots,b_n$$$ ($$$1\le b_i\le n+1$$$) — догадка Боба, где $$$b_i$$$ равно $$$i$$$-у цвету в его коде.
Гарантируется что сумма всех $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных в первой строке выведите «YES», если существует решение или «NO», если не существует ни одного секретного кода Алисы, соответствующего данной ситуации. Вы можете вывести каждый символ в любом регистре (верхнем или нижнем).
Если ответ «YES», на следующей строке выведите $$$n$$$ целых чисел $$$a_1,\ldots,a_n$$$ ($$$1\le a_i\le n+1$$$) — секретный код Алисы, где $$$a_i$$$ равно $$$i$$$-у цвету этого кода.
Если существует несколько возможных решений, выведите любое.
7 5 2 4 3 1 1 2 5 5 3 4 1 1 2 1 2 4 0 4 5 5 3 3 4 1 4 2 3 2 3 6 1 2 3 2 1 1 1 1 6 2 4 3 3 2 1 1 1 6 2 6 1 1 3 2 1 1
YES 3 1 6 1 2 YES 3 1 1 1 2 YES 3 3 5 5 NO YES 4 4 4 4 3 1 YES 3 1 3 1 7 7 YES 2 3 1 1 1 1
Первый набор входных данных описан в условии.
Во втором наборе в входных данных $$$x=3$$$, потому что цвета совпадают на позициях $$$2,4,5$$$. И $$$y=4$$$, потому что цвета $$$1,1,1,2$$$ общие у двух кодов.
В третьем наборе входных данных $$$x=0$$$, потому что цвета не совпадают ни в одной из позиций. Но $$$y=4$$$, потому что цвета $$$3,3,5,5$$$ общие у двух кодов.
В четвертом наборе входных данных можно показать что ни одного подходящего секретного кода Алисы не существует.
| Название |
|---|




