| Codeforces Round 658 (Div. 1) |
|---|
| Закончено |
После того, как вы получили 13 вердиктов time-limit-exceeded по ужасной геометрической задаче, вы решили сделать расслабляющий перерыв и позаниматься оригами.
Есть лист бумаги в форме простого многоугольника с $$$n$$$ вершинами. Многоугольник может быть невыпуклым, но мы все знаем, что настоящий лист бумаги для оригами имеет свойство, что любая горизонтальная прямая пересекает границу многоугольника не больше, чем в двух точках.
Если вы согнете лист бумаги вдоль вертикальной прямой $$$x=f$$$, какой будет площать полученной фигуры? Когда вы сгибаете лист, часть бумаги слева от прямой симметрично отражается с правой стороны.
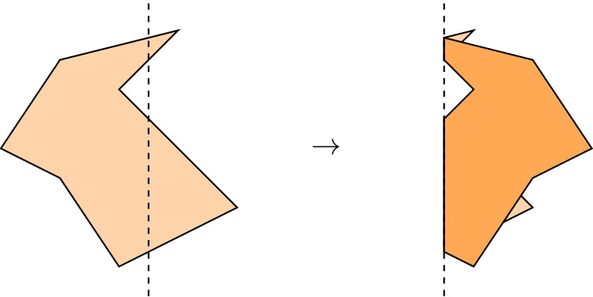
Ваша задача ответить на $$$q$$$ независимых запросов для значений $$$f_1,\ldots,f_q$$$.
В первой строке находится два целых числа $$$n$$$, $$$q$$$ ($$$3\le n\le 10^5, 1\le q\le 10^5$$$) — количество вершин многоугольника и количество запросов, соответственно.
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$x_i$$$, $$$y_i$$$ ($$$|x_i|, |y_i|\le 10^5$$$) — координаты $$$i$$$-й вершины многоугольника. Многоугольник состоит из отрезков, соединяющих пары соседних точек во входных данных и отрезка, соединяющего $$$(x_1,y_1)$$$ и $$$(x_n,y_n)$$$. Гарантируется, что многоугольник невырожденный, что любая горизонтальная прямая пересекает границу многоугольника в не более, чем двух точках. Также гарантируется, что ни одно ребро многоугольника не строго вертикальное. Соседние отрезки многоугольника могут быть параллельными.
Каждая из следующих $$$q$$$ строк содержит единственное целое число $$$f_i$$$ ($$$\min\limits_{j=1}^n(x_j)< f_i< \max\limits_{j=1}^n(x_j)$$$) — $$$x$$$-координата $$$i$$$-го запроса сгиба. Гарантируется, что все $$$f_i$$$ различны.
Для каждого запроса выведите площадь $$$A_i$$$ бумаги, которая будет, если согнуть лист бумаги вдоль прямой $$$x=f_i$$$.
Ваш ответ будет считаться правильным, если его абсолютная или относительная погрешность не превосходит $$$10^{-4}$$$.
Формально, пусть ваш ответ будет $$$a$$$, а ответ жюри будет $$$b$$$. Ваш ответ будет принят тогда и только тогда, когда $$$\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-4}$$$.
4 7 0 10 10 0 0 -10 -10 0 -9 -5 -1 0 1 5 9
199.0000000000 175.0000000000 119.0000000000 100.0000000000 119.0000000000 175.0000000000 199.0000000000
4 1 0 0 0 2 2 4 2 2 1
3.0000000000
9 4 0 -3 2 -2 -1 -1 0 4 2 5 1 6 -2 3 -1 1 -3 0 0 -2 -1 1
11.1250000000 11.7500000000 10.3446969697 11.3333333333
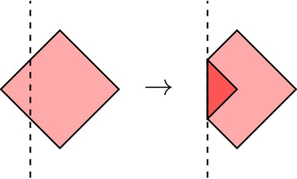
В первом тесте, если сделать сгиб в $$$f=-5$$$:
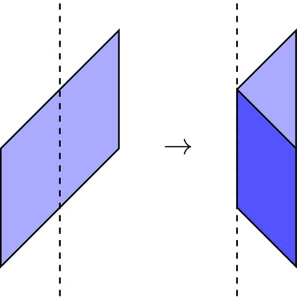
Во втором тесте, если сделать сгиб в $$$f=1$$$:
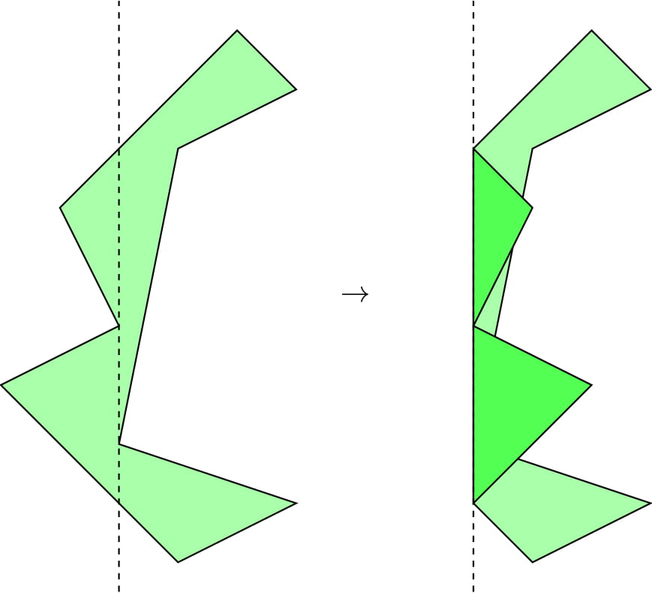
В третьем тесте, если сделать сгиб в $$$f=-1$$$:
| Название |
|---|




