| Codeforces Round 656 (Div. 3) |
|---|
| Закончено |
Вам задан граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер. Не гарантируется, что заданный граф связен. Некоторые ребра уже ориентированы и вы не можете менять их направление. Остальные ребра являются неориентированными и вам необходимо выбрать какое-то направление для всех этих ребер.
Вам необходимо ориентировать неориентированные ребра таким образом, что получившийся граф будет ориентированным и ацикличным (то есть графом, каждое ребро которого имеет ориентацию, а сам граф не имеет циклов). Заметьте, что вам необходимо ориентировать все неориентированные ребра.
Вам необходимо ответить на $$$t$$$ независимых наборов тестовых данных.
Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1 \le t \le 2 \cdot 10^4$$$) — количество наборов тестовых данных. Затем следуют $$$t$$$ наборов тестовых данных.
Первая строка набора тестовых данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$1 \le m \le min(2 \cdot 10^5, \frac{n(n-1)}{2})$$$) — количество вершин и количество ребер в графе, соответственно.
Следующие $$$m$$$ строк описывают ребра графа. $$$i$$$-е ребро представлено тройкой целых чисел $$$t_i$$$, $$$x_i$$$ и $$$y_i$$$ ($$$t_i \in [0; 1]$$$, $$$1 \le x_i, y_i \le n$$$) — типом ребра ($$$t_i = 0$$$, если ребро является неориентированным, и $$$t_i = 1$$$, если ребро является ориентированным) и вершинами, которые соединяет это ребро (неориентированное ребро соединяет вершины $$$x_i$$$ и $$$y_i$$$, а ориентированное ребро идет из вершины $$$x_i$$$ в вершину $$$y_i$$$). Гарантируется, что граф не содержит петель (ребер, идущих из вершину в саму себя) и кратных ребер (то есть для каждой пары ($$$x_i, y_i$$$) не существует других пар ($$$x_i, y_i$$$) или ($$$y_i, x_i$$$)).
Гарантируется, что сумма $$$n$$$ и сумма $$$m$$$ не превосходят $$$2 \cdot 10^5$$$ ($$$\sum n \le 2 \cdot 10^5$$$; $$$\sum m \le 2 \cdot 10^5$$$).
Выведите ответ на каждый набор тестовых данных — «NO», если невозможно ориентировать неориентированные ребра таким образом, чтобы получившийся граф был ориентированным и ацикличным, иначе выведите «YES» в первой строке, а затем $$$m$$$ строк, описывающие ребра получившегося ориентированного ацикличного графа (в любом порядке). Заметьте, что вы не можете менять направление уже ориентированных ребер. Если существует несколько ответов, выведите любой.
43 10 1 35 50 2 11 1 51 5 40 5 21 3 54 51 1 20 4 31 3 10 2 31 2 44 51 4 11 1 30 1 21 2 41 3 2
YES 3 1 YES 2 1 1 5 5 4 2 5 3 5 YES 1 2 3 4 3 1 3 2 2 4 NO
Объяснение второго набора тестовых данных примера:
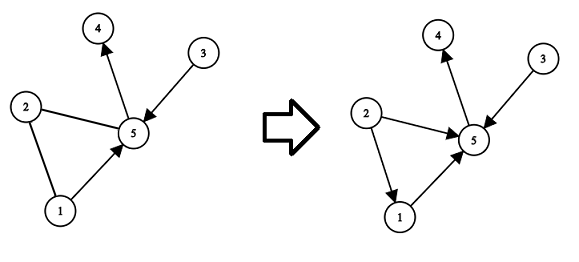
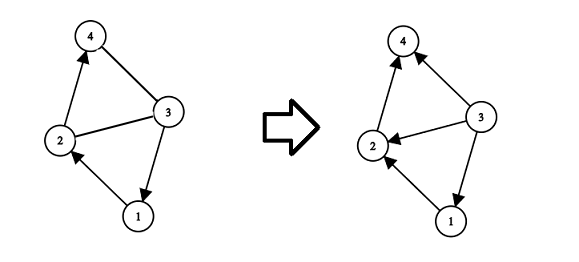
Объяснение третьего набора тестовых данных примера:
| Название |
|---|




