| Codeforces Round 656 (Div. 3) |
|---|
| Закончено |
Вам дано дерево (связный граф без циклов), состоящее из $$$n$$$ вершин. Дерево не является корневым — это просто неориентированный связный граф без циклов.
За один ход вы можете выбрать ровно $$$k$$$ листьев (лист — это такая вершина, которая соединена только с одной другой вершиной), соединенных с одной и той же вершиной, и удалить их вместе с ребрами, инцидентными им. То есть вы выбираете такие листья $$$u_1, u_2, \dots, u_k$$$, что существуют ребра $$$(u_1, v)$$$, $$$(u_2, v)$$$, $$$\dots$$$, $$$(u_k, v)$$$, и удаляете эти листья вместе с этими ребрами.
Ваша задача — найти максимальное количество ходов, которое вы можете совершить, если вы будете удалять листья оптимально.
Вам необходимо ответить на $$$t$$$ независимых наборов тестовых данных.
Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1 \le t \le 2 \cdot 10^4$$$) — количество наборов тестовых данных. Затем следуют $$$t$$$ наборов тестовых данных.
Первая строка набора тестовых данных содержит два целых числа $$$n$$$ и $$$k$$$ ($$$2 \le n \le 2 \cdot 10^5$$$; $$$1 \le k < n$$$) — количество вершин в дереве и количество листьев, которые вы удаляете за один ход, соответственно. Следующие $$$n-1$$$ строк описывают ребра. $$$i$$$-е ребро представлено в виде пары целых чисел $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le n$$$), где $$$x_i$$$ и $$$y_i$$$ — это вершины, которые соединяет $$$i$$$-е ребро. Гарантируется, что заданный набор ребер образует дерево.
Гарантируется, что сумма $$$n$$$ не превосходит $$$2 \cdot 10^5$$$ ($$$\sum n \le 2 \cdot 10^5$$$).
Выведите ответ на каждый набор тестовых данных — максимальное количество ходов, которое вы можете совершить, если вы будете удалять листья оптимально.
4 8 3 1 2 1 5 7 6 6 8 3 1 6 4 6 1 10 3 1 2 1 10 2 3 1 5 1 6 2 4 7 10 10 9 8 10 7 2 3 1 4 5 3 6 7 4 1 2 1 4 5 1 1 2 2 3 4 3 5 3
2 3 3 4
Картинка, соответствующая первому набору тестовых данных примера:
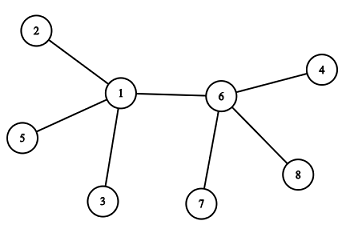
Здесь вы можете удалить вершины $$$2$$$, $$$5$$$ и $$$3$$$ в течение первого хода и вершины $$$1$$$, $$$7$$$ и $$$4$$$ в течение второго хода.
Картинка, соответствующая второму набору тестовых данных примера:
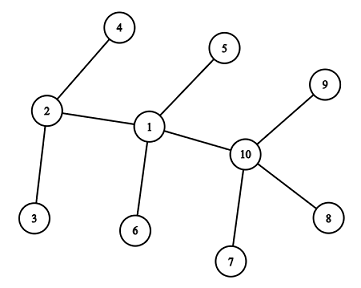
Здесь вы можете удалить вершины $$$7$$$, $$$8$$$ и $$$9$$$ в течение первого хода, затем вершины $$$5$$$, $$$6$$$ и $$$10$$$ в течение второго хода, и вершины $$$1$$$, $$$3$$$ и $$$4$$$ в течение третьего хода.
Картинка, соответствующая третьему набору тестовых данных примера:
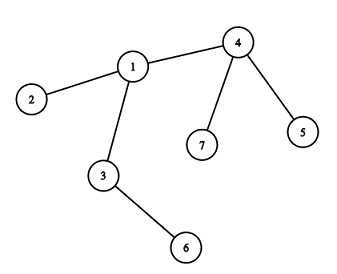
Здесь вы можете удалить вершины $$$5$$$ и $$$7$$$ в течение первого хода, затем вершины $$$2$$$ и $$$4$$$ в течение второго хода, и вершины $$$1$$$ и $$$6$$$ в течение третьего хода.
| Название |
|---|




