Джокер вернулся в Готэм-Сити для осуществления очередного злодейского плана. В Готэм-Сити есть $$$N$$$ перекрёстков (пронумерованных от $$$1$$$ до $$$N$$$) и $$$M$$$ дорог (пронумерованных от $$$1$$$ до $$$M$$$). Каждая улица соединяет два различных перекрёстка, и любые два перекрёстка соединены не более одной улицей.
Для своего злодейского плана, Джокеру нужно использовать нечётное количество улиц, которые образуют цикл. Формально, для перекрёстка $$$S$$$ и чётного натурального $$$k$$$, должна существовать такая последовательность перекрёстков $$$S, s_1, \ldots, s_k, S$$$, что есть улицы, соединяющие перекрёстки (a) $$$S$$$ и $$$s_1$$$, (b) $$$s_k$$$ и $$$S$$$, и (c) $$$s_{i-1}$$$ и $$$s_i$$$ для каждого $$$i = 2, \ldots, k$$$.
Однако, полиция патрулирует улицы Готэм-Сити. Каждый день $$$i$$$, она наблюдает за конкретным подмножеством улиц с последовательными номерами $$$j$$$: $$$l_i \leq j \leq r_i$$$. Эти улицы под наблюдением не могут быть использованы Джокером для своего плана в этот день. К несчастью для полиции, у Джокера есть шпионы среди Отделения Полиции Готэм-Сити; они доносят ему, в какие дни за какими улицами ведётся наблюдение. Теперь Джокер хочет узнать для некоторого количества дней, может ли он провернуть свой план в каждый из этих дней или нет. План может быть осуществлён, если есть цикл с нечётным количеством улиц, которые не находятся под наблюдением в данный день.
Первая строка ввода содержит три целых числа $$$N$$$, $$$M$$$ и $$$Q$$$ ($$$1 \leq N, M, Q \leq 200\,000$$$): количество перекрёстков, улиц и интересующих дней, соответственно. Следующие $$$M$$$ строк содержат описание улиц. $$$j$$$-я из этих строк ($$$1 \le j \le M$$$) содержит номера двух улиц $$$u$$$ и $$$v$$$ ($$$u \neq v$$$), что означает, что улица $$$j$$$ соединяет эти два перекрёстка. Гарантируется, что любые два перекрёстка соединены не более одной улицей. Каждая из следующих $$$Q$$$ строк содержит по двум целым числам $$$l_i$$$ и $$$r_i$$$, что означает, что в день $$$i$$$ ($$$1 \leq i \leq Q$$$) под наблюдением полиции находятся все улицы $$$j$$$ с номерами $$$l_i \leq j \leq r_i$$$.
Выведите $$$Q$$$ строк. $$$i$$$-я строка ($$$1 \leq i \leq Q$$$) должна содержать «YES», если Джокер может осуществить план в день $$$i$$$, и «NO» иначе.
Подзадачи:
- (6 баллов) $$$1 \leq N, M, Q \leq 200$$$
- (8 баллов) $$$1 \leq N, M, Q \leq 2\,000$$$
- (25 баллов) $$$l_i = 1$$$ для $$$i = 1, \ldots, Q$$$
- (10 баллов) $$$l_i \leq 200$$$ для $$$i = 1, \ldots, Q$$$
- (22 баллов) $$$Q \leq 2\,000$$$
- (29 баллов) Без дополнительных ограничений.
6 8 2 1 3 1 5 1 6 2 5 2 6 3 4 3 5 5 6 4 8 4 7
NO YES
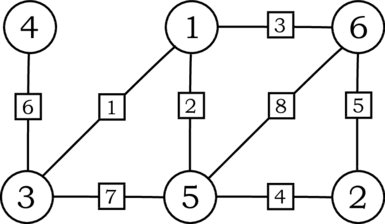
Граф из данного примера:
| Название |
|---|




